基本介紹
- 中文名:空子集
- 外文名:empty set
- 統稱:空集
- 符號表示:∅或{}
- 概述:不含A的元素的子集
- 領域:集合論
定義
子集


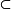
空子集


性質

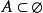
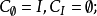



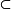



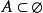
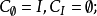

對於兩個集合A,B,如果A中任意一個元素都是B中的元素,我們就說這兩個集合有包含關係,稱集合A是集合B的子集(subset)(集合 A的空子集定義為不含A的元素的子...
(subset),如果集合B中有一個或以上的元素不屬於集合A,且集合A中的元素全部屬於集合B,那么我們說集合A是集合B的真子集,不包含元素的集合叫做空集(empty set),...
子集是一個數學概念:如果集合A的任意一個元素都是集合B的元素,那么集合A稱為集合B的子集。符號語言:若∀a∈A,均有a∈B,則A⊆B。...
別集名。明李夢陽(號空同子)作。六十六卷。凡賦三卷,詩三十四卷,文二十九卷。有明萬曆三十年鄧雲霄刻本,明刻曹大章重修本題《崆峒集》,清《四庫全書》...
在凸幾何中,凸集(convex set)是在凸組合下閉合的仿射空間的子集。更具體地說,在歐氏空間中,凸集是對於集合內的每一對點,連線該對點的直線段上的每個點也在該...
集合覆蓋有多個義項,它可以指集合論中的一個概念,在集合論中, 集合的覆蓋推廣了集合劃分的概念,其定義如下,設A是集合,如果這些非空子集的並集等於A,則由A的...
。(把離散拓撲放置到給定集合上的函子 左伴隨於 。)密著拓撲基本原理 編輯 在拓撲學中,帶有密著拓撲(trivial topology)的拓撲空間是其中僅有的開集是空集和整個...
但是這兩個數集都不具備性質5,例如所有形如nm(m>n,m,n 都是自然數)的數組成的集合是有理數集的非空子集,這個集合就沒有最小數;開區間(0,1)是實數集合...
設R是整環,若存在R°=R\{0}到非負整數集內的一個映射δ適合條件:任給a...單位元.環R的一個非空子集合S,若對R的加法、乘法也構成環,則稱S是R的子...
設S是線性空間E的一個非空子集,如果S中任何有限個元都是線性無關的,則稱S為E的一個線性無關的集合。...
集合X 的劃分是 X 的非空子集的集合,使得所有 X 的元素 x 都精確在這些子集的其中一個內。等價的說,X 的子集的集合 P 是X 的劃分,如果...
準確的定義:“對任意非空集合x,x至少有一元素y使x∩y為空集。”注:(ZF3)可以由其他公理導出,所以有些場合不出現這條公理,與之類似的是“子集公理”。...
