穆爾空間是拓撲學中的一種拓撲空間。設{2l}是拓撲空間X的開覆蓋列.對任意二EX,
基本介紹
- 中文名:穆爾空間
- 外文名:Moore space
- 所屬學科:拓撲學
定義

性質
概念
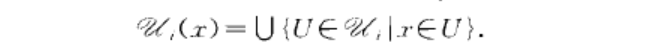
穆爾空間是拓撲學中的一種拓撲空間。設{2l}是拓撲空間X的開覆蓋列.對任意二EX,

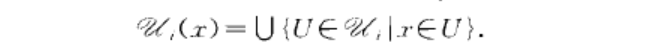
穆爾空間是拓撲學中的一種拓撲空間。設{2l}是拓撲空間X的開覆蓋列.對任意二EX,定義設n≥1,π為阿貝爾群。連通CW復形X=M(π,n)若滿足則稱M(π,n)為穆爾空間。性質度量空間必是穆爾空間。概念穆爾空間(Moor...
上半連續分解空間(upper semi-continuous decomposition space)是一類拓撲空間。商空間是上半連續分解空間的充分必要條件是自然映射為閉映射。上半連續分解空間的概念是穆爾(Moore,R.L.)於20世紀20年代末期引入的。概念 上半連續分解空間...
穆爾半平面(Moore semiplane)亦稱乃米茨基切圓盤空間,是一類特殊的拓撲空間。設X為包含二軸的上半平面,普通的開集在X上是開的,x軸上點P的鄰域基中的元素是在x軸的上方與點P相切的開圓盤與{P}的並集.拓撲空間X稱為穆爾半平面....
第五章 空間桁架 第六章 球形空間桁架 第三部分 框架系統 第七章 柱與牆 第八章 梁與板 第九章 框架 第四部分 懸索系統 第十章 懸索 第十一章 帳篷 第十二章 充氣式構造 第十三章 拱 第十四章 拱頂 第五部分 ...
穆爾在書中全方位地展現了建築在精神層面的價值內涵,也為人們體認自身提供了一面鏡子。作品目錄 第一章 欲望塑造空間,空間塑造欲望 第二章 固定的家和流浪的家 第三章 真實的冒牌貨 第四章 不連貫的地平線,或建築中的情色註解 ...
謎題趣味性強,且能鍛鍊學生的空間想像能力、邏輯推理能力、數學計算能力等多方面的思維能力,適合國小和國中低年級的學生閱讀與學習。圖書目錄 《逃出金字塔》《逃出叢林》《逃離海底》《逃離月球》作者簡介 加雷思·穆爾,熱銷腦力訓練圖書...
靈族人相信他們的家鄉和他們的古代文明的分布程度,從前覆蓋了整個恐懼之眼,在墮落期間混沌(Chaos)之力占據了整個空間領域。今日;恐懼之眼是所有已知地方中,異次元空間與真實空間重疊最大的一塊,在那裡混沌之力與所有物質宇宙混合在...
三十五首西洋藝術歌曲的演唱和伴奏 《三十五首西洋藝術歌曲的演唱和伴奏》是一本圖書,作者是傑拉爾德·穆爾
這一次,美麗幹練的媽媽卡珊德拉·瑞恩斯(史蒂芬·穆爾 Stephanie Moore 飾)和女兒安娜在林間遭到襲擊。當她醒來時,發現自己喪失部分記憶,身處一個隔絕密閉的空間。她好不容易找到另外四名受困的陌生人,並和他們策劃逃脫,誰知設施內...
“信息空間”的獨特之處是什麼?在信急空間中制定戰略 不斷擴展的地盤――諸多生態系統之家 美國電報電話公司和商業生態系統 你為哪些生態系統作貢獻?第三章 領導商業生態系統 制定戰略應著眼於創建新的微觀經濟和財富 價值和影響成為...
《星球大戰6:傳承》是2018年世界圖書出版公司出版的圖書。內容簡介 凱德·天行者一行人在旅途中突然被一股神秘的牽引力拽入了未知空間,在那裡等待他們的是一位曾隸屬共和國的絕地武士——塞萊斯特·莫內。她與一位名叫卡尼斯·穆爾的...
