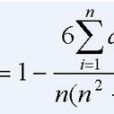秩相關係數（Coefficient of Rank Correlation），又稱等級相關係數，是將兩要素的樣本值按數據的大小順序排列位次，以各要素樣本值的位次代替實際數據而求得的一種統計量。它是反映等級相關程度的統計分析指標，常用的等級相關分析方法有Spearman相關係數和Kendall相關係數等。
基本介紹
- 中文名：秩相關係數
- 外文名：Coefficient of Rank Correlation
- 定義：反映等級相關程度的統計分析指標
- 別稱：等級相關係數
- 學科：統計學
簡介,計算方法,示例,相關檢驗,
簡介
秩相關係數，亦稱為“等級相關係數”，是反映等級相關程度的統計分析指標。常用的等級相關分析方法有Spearman相關係數和等。
如果秩相關係數為正，則
隨著
的增加而增加；如果秩相關係數為負，則隨著的增加而減小；如果秩相關係數為0，則表示隨著 的增加， 沒有增大或減小的趨勢。當 和 越來越接近嚴格單調的函式關係時，秩相關係數在數值上就越來越大。當秩相關係數為1或者-1時，就表明和之間嚴格單調增加或者嚴格單調減小。
在實際套用中，有時獲得的原始資料沒有具體的數據表現，只能用等級來描述某種現象，要分析現象之間的相關關係，就只能用秩相關係數。
計算方法
秩相關係數的計算步驟如下：
2）按順序求出兩個標誌的每對等級編號的差；
3）按下式計算相關係數：
示例
例如，2003年中國大陸各省（直轄市、自治區）的GDP（ ）和總人口（ ）數據及其位次，可以計算出來，將相應數據代入公式，就可以計算它們之間的秩相關係數。
相關檢驗
將
的絕對值同spearman相關係數統計表中的臨界值
進行比較。如果
，則表明變化趨勢有顯著意義；如果
，則表明變化趨勢沒有顯著意義；如果 為正值，則表明有上升趨勢；如果 為負值，則表明有下降趨勢。秩相關係數 檢驗的臨界值表如下：
表1.秩相關係數檢驗的臨界值表
n | 顯著水平α | 顯著水平α | n | 顯著水平α | 顯著水平α |
0.05 | 0.01 | 0.05 | 0.01 | ||
4 | 1.000 | -- | 16 | 0.425 | 0.601 |
5 | 0.900 | 1.000 | 18 | 0.399 | 0.564 |
6 | 0.829 | 0.943 | 20 | 0.377 | 0.534 |
7 | 0.714 | 0.893 | 22 | 0.359 | 0.508 |
8 | 0.643 | 0.833 | 24 | 0.343 | 0.485 |
9 | 0.600 | 0.783 | 26 | 0.329 | 0.465 |
10 | 0.564 | 0.746 | 28 | 0.317 | 0.448 |
12 | 0.456 | 0.712 | 30 | 0.306 | 0.432 |
14 | 0.456 | 0.645 | -- | -- | -- |
