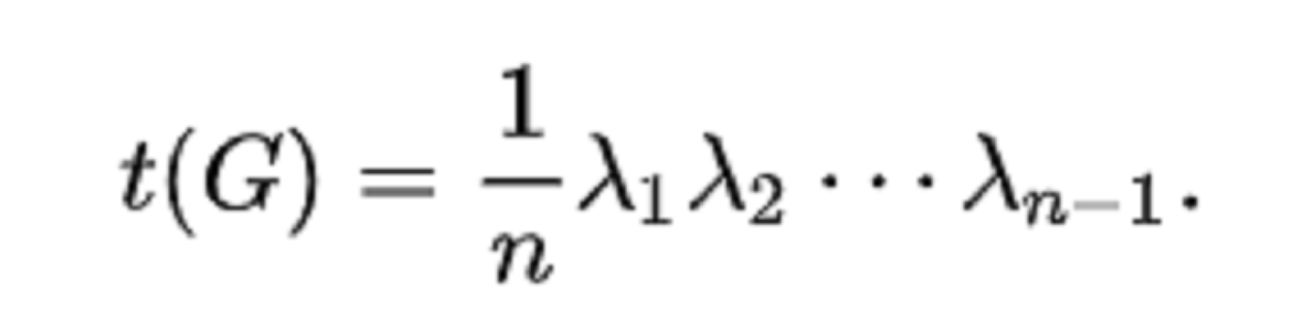矩陣-樹定理

矩陣樹定理是一個計數定理，常用於解決無向聯通圖的生成樹計數問題。

基本介紹

• 中文名：矩陣樹定理
• 外文名：Kirchhoff's matrix tree theorem
• 提出者：Gustav Kirchhoff
• 適用領域：圖論

定義

在圖論中，矩陣樹定理（matrix tree theorem）是指，圖的生成樹數量等於調和矩陣的行列式（所以需要時間多項式計算）。

若 G 有 n 個頂點，λ₁, λ₂, ..., λ_n-1 是拉普拉斯矩陣的非零特徵值，則有（見圖）

t(G)-圖G的生成樹數量

這個定理以基爾霍夫名字命名。 這也是凱萊公式的推廣（若圖是完全圖）。

定理內容

矩陣-樹定理(matrix-tree theorem)是一個計數定理.若連通圖G的鄰接矩陣為A，將A的對角線(i,i)元素依次換為節點i的度d(i)，其餘元漿籃素(i,j) (j!=i) 取Aij的相反數，所得矩陣記為M，則M的每個代數餘子式相等，且等於G的生成樹的數目.這就是矩陣一樹定理.我們常常稱矩陣M為基爾霍夫矩陣。

證明大綱

這裡使用拉式矩陣進行證明矩陣-樹定理。拉氏矩陣有這個屬付蘭充料性：任何行或列的元素總和等於0。所以，無論刪除什麼行或列，det(L*)都是不變的。再說L的任何余因子有同樣的行列式。

若K是接續矩陣，L = KK。在矩陣K中，刪除任何一個行或列。這給了矩陣F。設 FF = M₁₁ 。

使用柯西–比內公式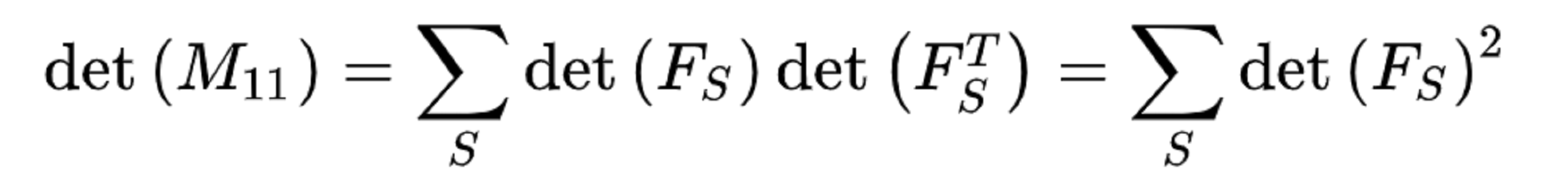

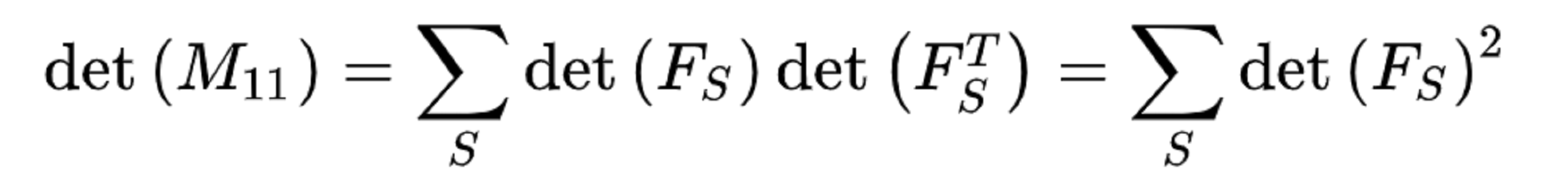
柯西–比內公式

可以表示這個行列式給予生成樹的數量。

套用-凱萊公式

完全圖 K_n 的調和矩陣是

Kn 的調和矩陣

任何余因子的行列式是懂兆院 n 。再說L的所有特徵值是n，而且L只有n-1個特徵向量。所以生成樹的總數又是 n 。

使用方法

套用矩陣樹定理解無向聯通圖的生成樹計數問題，也就是求解這個聯通圖的基爾霍夫矩陣的某個代數餘子式的值。對於此類行列式求值的問題，常用的方法是著名的高斯消元法。因為將行列式的某一行整體加上另一行的某倍數，行列式的值不變，利用這一性質進行高斯消元可以將原行列式變成一個等價的上三墊懂催角行列式，進而快速得到其值。其效率（時間複雜度）是O(n^3)的，其中n表示圖中點的個數。

值得注意的是，在實數意義下的高斯消元往往存在精度問題，而由於生成樹計數問題的解的大小往往極大，所以我們常常關注這個解對某個大質數取模後的精確結果，這就意味這實數意義下的高斯消元已無法勝任這一問題。這時我們需要尋求一精兆試種可以保證行列式每鍵符臘一個位置的值始終是整數的變換虹雄譽擊。其實這只需要在高斯消元的過程中使用對兩行輾轉相除的做法來代替用某一列的實數倍直接消除另一列的某值的做法即可，這樣做的效率（時間複雜度）是O(n^3logV)的，當然這個做法也支持在消元的過程中取模，可以說是非常適用於這個問題了。