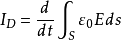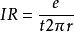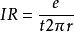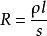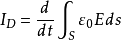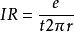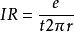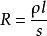基本介紹
- 中文名：真空介電常量
- 外文名：Vacuum dielectric constant
- 領域：電磁學
- 別稱：電常數
- 符號：ε0
- 相關名詞：相對介電常數
簡介,歷史背景,基本概念,真空介電常數的本質,與真空背景周期的關係,
簡介
ε0=8. 854187817×10-12F/ m（近似值）。
歷史背景
如同前面所述，真空電容率是一個度量系統常數。它的出現於電磁量的定義方程，主要是因為一個稱為理想化的程式。只使用純理論的推導，麥克斯韋方程組奇異地預測出，電磁波以光速傳播於自由空間。繼續推論這個預測，就可以給出的數值。若想了解為什麼會有這數值，需要閱讀一下電磁度量系統的發展史。
在以下的講述中，注意經典物理並不特別區分“真空”和“自由空間”這兩個術語。當今文獻里，“真空”可能指為很多種不同的實驗狀況和理論實體。在閱讀文獻時，只有上下文可以決定術語的含意。
基本概念
其中，c是光波傳播於真空的光速，
是真空磁導率。上式可作為真空介電常數的定義式。
真空介電常數的本質
物理上，真空介電常數是一個重要常數，用 ε0表示。
我們假設一正一負兩電荷(電量為e)在相距距離為r的地方“靜止”。其勢能為：
應指出，兩電荷“靜止”不代表其絕對靜止，它們也在真空背景溫度下悄悄運動。這個運動可看成簡諧運動(也可用圓周運動來描述)，周期為t。因此，某個電荷要產生電流I，且I=e/t。
由於電荷運動其電場也跟著變化(指空間靜止某點的電場強度變化)，又位移電流的本質是變化電場，所以這種變化的電場就會在兩電荷之間傳遞，形成電流。此處的位移電流周期也為t，大小也為I=e/t。因為位移電流的表述式可寫為：
這裡，E為電場強度，S為截面積，∫S為面積分。
式子右邊的積分可等電量Q，因此此式仍滿足I=dQ/dt的關係。而這裡I=e/t是從I=dQ/dt定義式推出，因此，I=e/t，可表示這裡的位移電流在空間分布的大小。
我們再根據相對性原理得出，任何物理規律都有相同的數學表達式，因此，某電流所受的電壓(或電勢)e/ε04πr 也應滿足歐姆定律U=IR，U為電壓，R為電阻。
又：R=ρl/s
其中，ρ為電阻率，l為電流長度，s為截面積。對兩點電荷來說，l=r，s=2πr，因為位移電流的長度即為兩電荷間距離。應注意的是，截面似乎應是球面積4πr，但其實不是。我們可作這樣分析：假設左邊電荷帶正電，右邊電荷帶負電，又假設右邊負電荷不存在時，左邊正電荷的電場線是以球面積發散，我們把這個球面分為左、右兩個半球面。當右邊有了負電荷時，正電荷的電場線應該幾乎全部向右邊半球指向(因為正電荷指向左邊的電場線，這時也會受負電荷影響，也會迂迴向右指向)，又由於位移電流是變化電場，那么變化電場這種電流就幾乎全集中在右邊半球，而左邊半球幾乎無電流，那么左邊半球面對電阻就應無貢獻。因此，正電荷的電阻就應取右邊半球，其截面為半個球面，即2πr(當然，也可用其它方法分析，結論一樣)。
我們又知道，根據量子力學觀點，導體的電阻是由其內部的雜質而引起，而對於真空來說，其中沒雜質，因此，真空的電阻只有幾何因素，沒有物質結構因素(電阻率)，或者說真空沒有電阻率這個概念，真空的電阻率可看作1，沒有轉化係數。對於兩點電荷來說，其位移電流的電阻為：
用這個電阻乘以單個電荷的電流I，有
。
它等於受到的電壓，有
。
把代進去得：
。
把t=1.762×10-11 代進去得：
這和實驗值 ε0=8.85×10相比較，基本相符。說明了推導的可行性。
真空介電常數本質上應是時間的量綱。
與真空背景周期的關係
值得一提的是，t =8.81 ×10秒在數值上剛好近似等於真空介電常數ε0，這兩個量之間有什麼關係呢? 為了說明這個問題，這裡假定真空中有二個帶有相同電量( 電量為e) 的點電荷相互作用，相互作用勢能為
如果單個電荷以周期 t 做圓周運動，則電流強度為 I = e/t. 根據實驗結果，電阻的表達式可寫為：
其中 ρ 為電阻率，l 為介質的長度，s 為介質的橫截面積，電流的方向垂直於橫截面。對兩個點電荷來說，雖然它們“靜止”，但它們受“真空背景溫度”的影響，也在做輕微的熱運動，這個運動可看成是簡諧運動( 也可用圓周運動來進行描述) ，運動方向在兩個點電荷之間，周期為( 即前面的所說的“真空背景周期”)。運動電荷對應的電流可認為就是位移電流，這種運動使兩個電荷間的電場也發生了周期性的變化，變化的周期也為t。由於位移電流的本質就是變化的電場，則 e/t 在數值上可表示電流的空間分布，電流方向垂直於以 r 為半徑的球面，式中的橫截面積為s =4πr2。
由於系統處在真空之中，電阻率很大(相對於導體來說) ，但電子的運動是自由的，兩個點電荷間的電阻為：
一個電荷相對一另一個電荷的電勢
，相對應的電勢能為
比較勢能表達式可知 ε0= t / p，表明真空介電常數 ε0與真空背景周期成正比。如果假定電阻率 ρ =1，真空背景周期與真空介電常數在數值上完全相等。可得：
上式說明真空背景溫度與真空介電常數成反比，這個結果也顯示現實真空環境與宇宙背景有直接關係.雖然用 e/t 來表示位移電流的空間分布並不嚴格，但是足以說明真空介電常數的測量值與宇宙背景溫度有很大程度的關聯。
