基本介紹
- 中文名:直線公理
- 外文名:linear axiom
- 所屬學科:數學(初等幾何)
- 簡要介紹:兩點確定一條直線
- 相關知識:直線,直線相交等
基本內容,套用舉例,直線的相關公理,阿基米德公理,稠密性公理,連續性公理,
基本內容
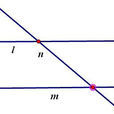
直線的基本性質(公理): (1)經過兩點有一條直線,並且只有一條直線。(2)兩條直線相交,只有一個交點。因為直線是不定義的名詞,對直線概念的理解往往靠上述的基本性質。
套用舉例
【例1】已知點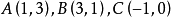 ,求
,求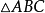 的面積。
的面積。
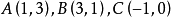
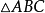
 圖1
圖1解: 如圖1,設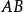 邊上的高為
邊上的高為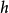 ,則
,則
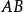
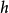
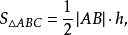
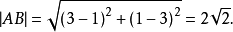
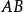

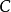
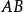
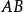

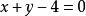
點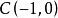 到
到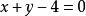 的距離
的距離
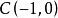
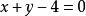

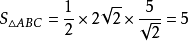
實際上,在以上解法中求直線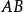 的方程可以不用兩點式,可以運用直線公理“兩點確定一條直線”通過觀察簡潔求解:
的方程可以不用兩點式,可以運用直線公理“兩點確定一條直線”通過觀察簡潔求解:
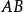
由點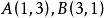 及
及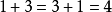 ,得點
,得點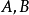 均在直線
均在直線
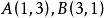
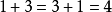
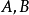
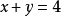
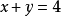
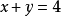
【例2】 已知兩條相交直線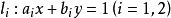 的交點是(5,3),求過兩點
的交點是(5,3),求過兩點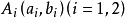 的直線的方程。
的直線的方程。
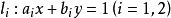
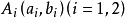
解:可得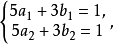 所以
所以 (否則
(否則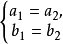 ,兩條直線
,兩條直線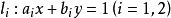 重合),把兩個等式相減,得
重合),把兩個等式相減,得
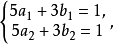

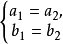
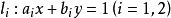
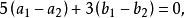
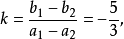
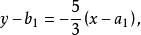
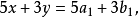
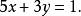
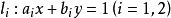
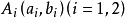

由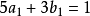 知,點,
知,點,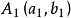 在直線
在直線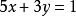 上;由
上;由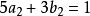 知,點
知,點 也在直線
也在直線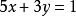 上,所以由“兩點確定一條直線”知,直線
上,所以由“兩點確定一條直線”知,直線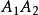 就是直線
就是直線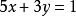 ,即直線
,即直線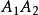 的方程是
的方程是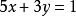 。
。
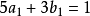
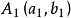
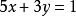
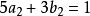

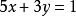
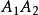
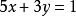
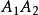
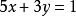
直線的相關公理
關於直線的基本性質,是用下面一組公理描述的。
阿基米德公理
對於任意線段 ,如圖2,存在一個自然數
,如圖2,存在一個自然數 ,使得
,使得


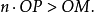
 圖2
圖2阿基米德公理是說,無論線段OP如何小,點M離點O無論多遠,用線段OP在直線上連續截取足夠的次數,將得到終點Q,點Q在點M的右邊,即 。
。

稠密性公理
對於直線上任意兩個不同的點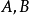 ,在直線上至少存在一點
,在直線上至少存在一點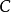 介於點A和點B之間,如圖3。
介於點A和點B之間,如圖3。
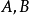
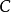
 圖3
圖3由公理很容易得到下面的推論。
推論 在直線上的點A與點B之間,存在著無限多個點。
連續性公理
對於直線上的線段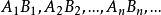 的無窮序列,如果滿足:
的無窮序列,如果滿足:
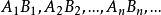
(1) 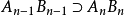 ;
;
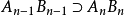
(2) 對於給定的任一小的線段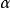 ,總存在一個數
,總存在一個數 使得
使得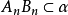 ,如圖4,
,如圖4,
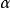

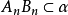
那么存在唯一的點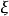 ,使得
,使得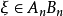 (對一切
(對一切 ),這個公理也叫做退縮線段原理,圖5是它的幾何解釋。
),這個公理也叫做退縮線段原理,圖5是它的幾何解釋。
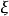
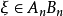

 圖4
圖4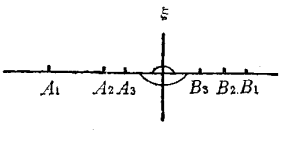 圖5
圖5