自由樹
自由樹就是一個無迴路的連通圖(沒有確定根)(在自由樹中選定一頂點做根,則成為一棵通常的樹)。從根開始,為每個頂點(在樹中通常稱作結點)的孩子規定從左到右的次序,則它就成為一棵有序樹。在圖的套用中,我們常常需要求給定圖的一個子圖,使該子圖是一棵樹。
生成樹
在圖論中,如果連通圖
的一個子圖是一棵包含
的所有頂點的樹,則該子圖稱為G的生成樹(SpanningTree)。
生成樹是連通圖的包含圖中的所有頂點的極小連通子圖。
圖的生成樹不惟一。從不同的頂點出發進行遍歷,可以得到不同的生成樹。
通用定義:
若從圖的某頂點出發,可以系統地訪問到圖中所有頂點,則遍歷時經過的邊和圖的所有頂點所構成的子圖,稱作該圖的生成樹。
(1)若G是強連通的有向圖,則從其中任一頂點v出發,都可以訪問遍G中的所有頂點,從而得到以v為根的生成樹。
(2)若G是有根的有向圖,設根為v,則從根v出發可以完成對G的遍歷,得到G的以v為根的生成樹。
(3)若G是非連通的無向圖,則要若干次從外部調用
DFS(或
BFS)算法,才能完成對G的遍歷。每一次外部調用,只能訪問到G的一個連通分量的頂點集,這些頂點和遍歷時所經過的邊構成了該連通分量的一棵DFS(或BPS)生成樹。G的各個連通分量的DFS(或BFS)生成樹組成了G的DFS(或BFS)生成森林。
(4)若G是非強連通的有向圖,且源點又不是有向圖的根,則遍歷時一般也只能得到該有向圖的生成森林。
分類
1)生成樹的求解方法
設圖
是一個具有n個頂點的連通圖。則從G的任一頂點(源點)出發,作一次深度優先搜尋(廣度優先搜尋),搜尋到的n個頂點和搜尋過程中從一個已訪問過的頂點
搜尋到一個未曾訪問過的鄰接點
,所經過的邊
(共n-1條)組成的極小連通子圖就是生成樹。(源點是生成樹的根)
通常,由深度優先搜尋得到的生成樹稱為深度優先生成樹,簡稱為DFS生成樹;由廣度優先搜尋得到的生成樹稱為廣度優先生成樹,簡稱為BFS生成樹。
注意:
①圖的廣度優先生成樹的樹高不會超過該圖其它生成樹的高度
②圖的生成樹不惟一,從不同的頂點出發進行遍歷,可以得到不同的生成樹。
最小生成樹
對於連通的帶權圖(連通網)G,其生成樹也是帶權的。生成樹T各邊的權值總和稱為該樹的權,記作:
其中,TE表示T的邊集,w(u,v)表示邊(u,v)的權。權最小的生成樹稱為G的最小生成樹(Minimum SpannirngTree)。最小生成樹可簡記為MST。
普里姆(PRIM)算法
算法簡單描述
1)輸入:一個加權連通圖,其中頂點集合為V,邊集合為E;
2)初始化:Vnew= {x},其中x為集合V中的任一節點(起始點),Enew= {},為空;
3)重複下列操作,直到Vnew= V:
a. 在集合E中選取權值最小的邊<u, v>,其中u為集合Vnew中的元素,而v不在Vnew集合當中,並且v∈V(如果存在有多條滿足前述條件即具有相同權值的邊,則可任意選取其中之一);
b. 將v加入集合Vnew中,將<u, v>邊加入集合Enew中;
4)輸出:使用集合Vnew和Enew來描述所得到的最小生成樹。
偽代碼描述
PrimMST(G,T,r) { //求圖G的以r為根的MST,結果放在T=(U,TE)中 InitCandidateSet(…);//初始化:設定初始的輕邊候選集,並置T=({r},¢) for(k=0;k<n-1;k++) { //求T的n-1條樹邊 (u,v)=SelectLiShtEdge(…);//選取輕邊(u,v); T←T∪{(u,v) }; //擴充T,即(u,v)塗紅加入TE,藍點v並人紅點集U ModifyCandidateSet(…); //根據新紅點v調整候選輕邊集 } } 用普里姆算法構造最小生成樹的過程
用普里姆算法構造最小生成樹的過程克魯斯卡爾(Kruskal) 算法
Kruskal算法是基於貪心的思想得到的。首先我們把所有的邊按照權值先從小到大排列,接著按照順序選取每條邊,如果這條邊的兩個端點不屬於同一集合,那么就將它們合併,直到所有的點都屬於同一個集合為止。至於怎么合併到一個集合,那么這裡我們就可以用到一個工具——-並查集。換而言之,Kruskal算法就是基於並查集的貪心算法。
算法流程:
輸入:圖G
輸出:圖G的最小生成樹
具體流程:
1)將圖G看做一個森林,每個頂點為一棵獨立的樹
2)將所有的邊加入集合S,即一開始S=E
3)從S中拿出一條最短的邊(u,v),如果(u,v)不在同一棵樹內,則連線u,v合併這兩棵樹,同時將(u,v)加入生成樹的邊集E'
4)重複(3)直到所有點屬於同一棵樹,邊集E'就是一棵最小生成樹
時間複雜度:
Kruskal算法每次要從都要從剩餘的邊中選取一個最小的邊。通常我們要先對邊按權值從小到大排序,這一步的時間複雜度為為O(|Elog|E|)。Kruskal算法的實現通常使用並查集,來快速判斷兩個頂點是否屬於同一個集合。最壞的情況可能要枚舉完所有的邊,此時要循環|E|次,所以這一步的時間複雜度為O(|E|α(V)),其中α為Ackermann函式,其增長非常慢,我們可以視為常數。所以Kruskal算法的時間複雜度為O(|Elog|E|)。
 Kruskal算法構造最小生成樹的過程
Kruskal算法構造最小生成樹的過程套用
網路G表示n各城市之間的通信線路網線路(其中頂點表示城市,邊表示兩個城市之間的通信線路,邊上的權值表示線路的長度或造價。可通過求該網路的最小生成樹達到求解通信線路或總代價最小的最佳方案。
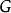
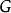
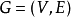
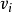



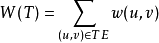
 用普里姆算法構造最小生成樹的過程
用普里姆算法構造最小生成樹的過程 Kruskal算法構造最小生成樹的過程
Kruskal算法構造最小生成樹的過程