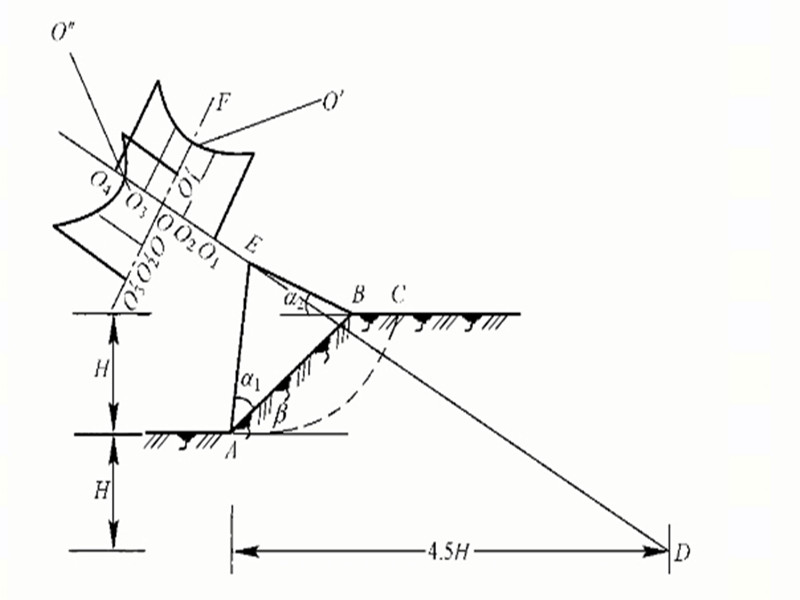
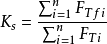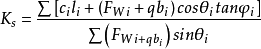一般計算公式
瑞典條分法假設滑動面為圓弧面,將滑動體分為若干個豎向土條,並忽略各土條之間的相互作用力。按照這一假設,任意土條只受自重力F
Wi、滑動面上的剪下力F
Ti和法向力F
Ni,如右圖1所示。將F
Wi分解為沿滑動面切向方向分力和垂直於切向的法向分力,並由第i條土的靜力平衡條件可得F
Ni=F
Wicosθ
i,其中,F
Wi=b
ih
i×γ
i。
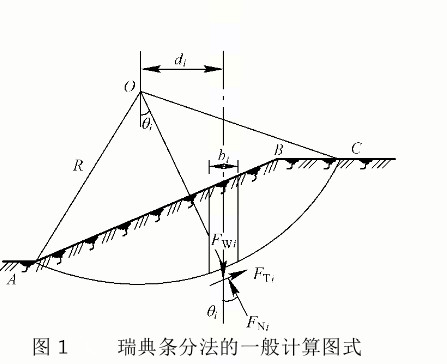 圖1
圖1設土坡安全係數為Ks,它等於第i個土條的安全係數,由庫侖強度理論有
式中,FTi———土條i在其滑動面上的抗滑力;
Ks———土坡和土條的安全係數。
按整體力矩平衡條件,滑動體ABC上所有外力對圓心的
力矩之和應為0。在各土條上作用的重力產生的滑動力矩之和為
滑動面上的法向力FNi通過圓心,不引起力矩,滑動面上設計剪力FTi產生的滑動力矩為
由於極限情況下抗滑力矩和滑動力矩相平衡;所以令上述兩式相等,則
這是最簡單的條分法的計算公式。由於忽略了土條之間的相互作用力;所以由土條上的3個力FWi、FTi和FNi組成的力多邊形不閉合,所以瑞典條分法不滿足靜力平衡條件,只滿足滑動土體的整體力矩平衡條件。儘管如此,由於計算結果偏於安全,在工程上仍有很廣泛的套用。
需要指明的是,使用瑞典條分法仍然要假設很多滑動面並通過試算分析,才能找到最小的Ks值,從而找到相應的最危險的滑動面。
相關分析
有孔隙水壓力作用時土坡穩定分析
當已知第i個土條在滑動面上的孔隙水壓力為u
i時(如圖2所示),要用有效指標c′
i及φ′
i代替原來的c
i和 φ
i。考慮土的有效強度,根據摩爾-庫侖強度理論,有
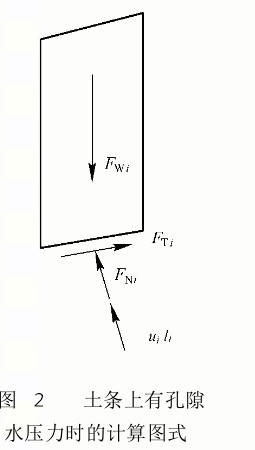 圖2
圖2取法線方向力的平衡,可得
各土條對圓弧中心O的力矩和為0,即
式中,xi———圓心O至FWi作用線的水平距離,xi=Rsinθi。
將式②代入式得
這就是用有效應力方法表示的瑞典條分法計算Ks的公式。
經過多年工程實踐,對瑞典條分法已積累了大量的經驗。用該法計算的安全係數一般比其他較嚴格的方法低10% ~20%;在滑動面圓弧半徑較大並且孔隙水壓力較大時,安全係數計算值估計會比其他較嚴格的方法小一半。因此,這種方法是偏於安全的。
坡頂有超載和土成層時穩定性分析
當土坡由多層土構成(如圖3所示),在使用公式①時應作必要的修正。
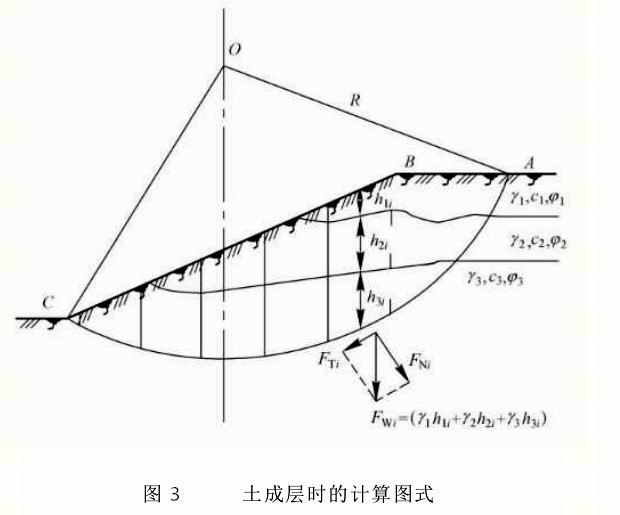 圖3
圖3(1)如果同一土條跨越多層土,計算其重量時應分層取相應的高度和厚度,計算相應重量後疊加。如第i個土條包括k層土,則
FWi=bi(γ1ih1i+γ2ih2i+…+γkihki)
(2)計算滑動面上的抗剪強度時,所用的土性參數c、φ應按土條滑動面所在的具體土層位置來選取相應的數值。如當第i個土條的滑動面在第m層內時,則
FTfi=cmilmi+FNitanφmi
當第i個土條的滑動面跨越m層土,則
FTfi=(c1il1i+c2il2i+…+cmilmi)+FNi(tanφ1i+tanφ2i+…+tanφmi)。
提示:FNi是第i條土滑動面上的法向反力之和,FNi=FWicosθi,與土條自重有關,而與滑動面上土層土性沒有直接關係。因此,對於成層土坡,可用下式計算其安全係數:
式中,FTi=FWisinθi
如果在土坡坡頂作用著超載q,如圖4所示,計算的基本原則和程式不變,只是在土條受力分析時,需要將土條上作用的超載加進土條的自重中去考慮;如果超載作用在坡面上,處理方法相似。當然可能某些土條上並沒有超載,則該土條僅考慮自重。當僅在坡頂有超載時,按下式計算安全係數,即
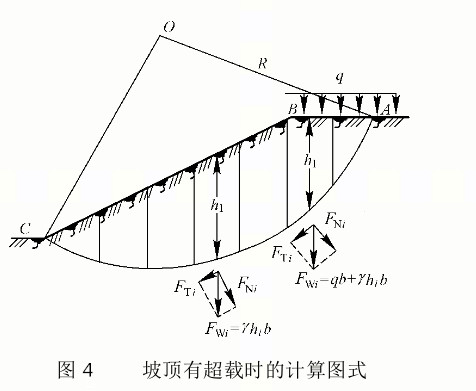
用條分法時簡單土坡最危險滑動面的確定
簡單土坡指的是土坡坡面單一、無變坡、土質均勻、無分層的土坡。如圖5所示,這種土坡最危險的滑動面可用以下方法快速求出。
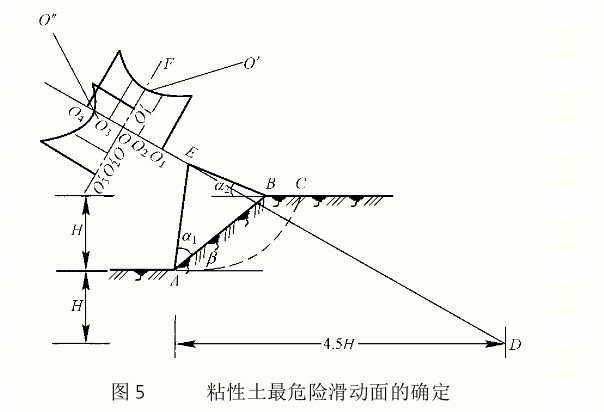
(1)根據土坡坡度或坡角β,由下表查出相應 α1、α2的數值。
(2)根據α1角,由坡腳A點作線段AE,使角∠EAB=α1;根據 α2角,由坡頂B點作線段BE,使該線段與水平線夾角為α2。
(3)線段AE與線段BE的交點為E,這一點是 φ=0的粘性土土坡最危險的滑動面的圓心。
(4)由坡腳A點豎直向下取坡高H值,然後向右沿水平方向線上取4.5H,並定義該點為D點。連線線段DE並向外延伸,在延長線上距E點附近,為 φ >0的粘性土坡最危險的滑動面的圓心位置。
(5)在DE的延長線上選3~5個點作為圓心O1、O2、O3…,計算各自的土坡穩定安全係數K1、K2、K3…。而後按一定的比例尺,將Ki的數值畫在過圓心Oi與DE正交的線上,並連成曲線(由於K1、K2、K3…數值一般不等)。取曲線下凹處的最低點O′,過O′作直線O′F與DE正交。O′F與DE相交於O點。
(6)同理,在O′F直線上,在靠近O點附近再選3~5個點,作為圓心O′1、O′2、O′3…,計算各自的土坡穩定安全係數K′1、K′2、K′3…。而後按相同的比例尺,將K′i的數值畫在通過各圓心O′i並與O′F正交的直線上,並連成曲線(因為K′1、K′2、K′3…數值一般不等)。取曲線下凹處的最低點O″點,該點即為所求最危險滑動面的圓心位置。
土坡坡度 | 坡角β | α1角 | α2角 |
1∶0.58 | 60° | 29° | 40° |
1∶1.0 | 45° | 28° | 37° |
1∶1.5 | 33°41′ | 26° | 35° |
1∶2.0 | 26°34′ | 25° | 35° |
1∶3.0 | 18°26′ | 25° | 35° |
1∶4.0 | 14°03′ | 25° | 36° |
 圖1
圖1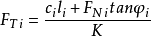
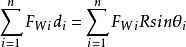
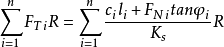
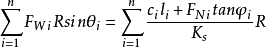
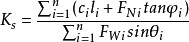
 圖2
圖2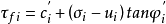
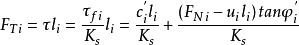
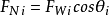
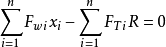
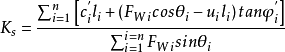
 圖3
圖3