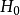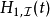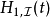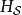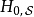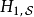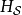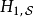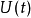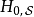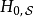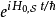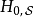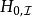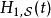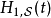狄拉克繪景

狄拉克繪景，又稱相互作用繪景。在量子力學里，相互作用繪景（interaction picture），是在薛丁格繪景與海森堡繪景之間的一種表述，為紀念物理學者保羅·狄拉克而又命名為狄拉克繪景。在這繪景里，描述量子系統的態矢量與表達可觀察量的算符都會隨著時間流易而演化。有些實際案例會涉及到因相互作用而使得量子態與可觀察量發生改變，這類案例通常會使用狄拉克繪景。

狄拉克繪景與薛丁格繪景、海森堡繪景不同。在薛丁格繪景里，描述量子系統的態矢量隨著時間流易而演化。在海森堡繪景里，表達可觀察量的算符會隨著時間流易而演化。

這三種繪景殊途同歸，所獲得的結果完全一致。這是必然的，因為它們都是在表達同樣的物理行為。

基本介紹

• 中文名：狄拉克繪景
• 外文名：interaction picture
• 領域：量子力學
• 別稱：相互作用繪景

定義

為了便利分析，位於下標的符號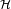 、 、 分別標記海森堡繪景、狄拉克繪景、薛丁格繪景。

通過對於基底的一種么正變換，算符和態矢量在狄拉克繪景里的形式與在薛丁格繪景里的形式相關聯。

在量子力學裡，對於大多數案例的哈密頓量，通常無法找到薛丁格方程的精確解，只有少數案例可以找到精確解。因此，為了要能夠解析其它沒有精確解的案例，必須將薛丁格繪景里的哈密頓量 分成兩個部分，

其中， 有精確解，有廣泛知悉的物理行為，而 則通常沒有精確解，是對於系統的攝動。

假若哈密頓量 含時（例如，感受到時變外電場作用的量子系統，其哈密頓量會含時），則通常會將顯性含時部分放在 里。這樣， 不含時，而時間演化算符 的公式可以簡單地表示為

其中，t是時間。

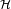
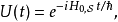
假若對於某些案例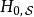， 應該設定為含時，則時間演化算符的公式會變得較為複雜：

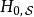
本條目以下內容假設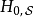 不含時。

態矢量

在狄拉克繪景里，態矢量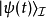 定義為

其中， 是在薛丁格繪景里的態矢量。

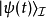
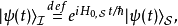
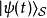
由於在薛丁格繪景里， 態矢量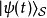 與時間的關係為

所以，在 對易的條件下，可以有

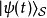
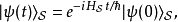
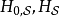
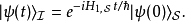
算符

在狄拉克繪景里的算符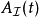 定義為

其中， 是在薛丁格繪景里對應的算符。（請注意， 通常不含時間，可以重寫為 。反例，對於時變外電場的狀況，哈密頓算符 含時。）

哈密頓算符

假若 不含時，則 與 對易，不論在薛丁格繪景里或在狄拉克繪景里， 與 的形式都是一樣：

所以，算符 與 都可以簡略標記為 ，不會造成歧意。

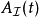
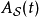
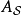
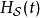
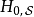
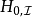
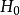
哈密頓算符的攝動成分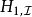 是

除非對易關係式 ，在狄拉克繪景里， 含時。

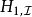
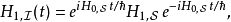
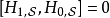
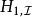
時間演化方程

本文以下內容，算符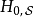 與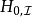 都簡略標記為 。

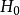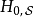
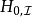
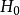
密度矩陣的時間演化

套用施溫格-朝永振一郎方程於密度矩陣，則可得到

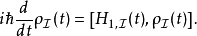
狄拉克繪景的套用

套用狄拉克繪景的目的是促使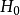與時間無關，只有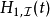與時間有關，也只有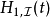控制態矢量隨時間流易的演化行為。

假若有精確解，而是一個弱小的攝動，則可很便利地採用狄拉克繪景，使用時變攝動理論來計算所產生對於整個系統的影響。例如，在費米黃金定則的導引里，或在推導戴森級數時，通常都會用到狄拉克繪景。

參閱

• 狄拉克標記
  
• 朱利安·施溫格
  
• 朝永振一郎