基本介紹
- 中文名:狄利克雷核
- 外文名:Dirichlet kernel
- 領域:數學
- 發明人:狄利克雷
- 性質:三角函式表示的積分核
- 表示符號:Dk(x)
狄利克雷簡介
狄利克雷核表述

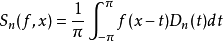


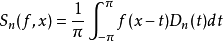

約翰·彼得·古斯塔夫·勒熱納·狄利克雷(Johann Peter Gustav Lejeune Dirichlet,勒熱納·狄利克雷是姓,1805年2月13日-1859年5月5日),德國數學家。他是解析數論...
狄利克雷函式(英語:dirichlet function)是一個定義在實數範圍上、值域不連續的函式。狄利克雷函式的圖像以Y軸為對稱軸,是一個偶函式,它處處不連續,處處極限不存在...
數學中,經典狄利克雷問題(classical Dirichlet problem)是尋找一個函式,使其為給定區域內一個指定的偏微分方程(PDE)的解,且在邊界上取預定值。...
狄利克雷分布(Dirichlet distribution)或多元Beta分布(multivariate Beta distribution)是一類在實數域以正單純形(standard simplex)為支撐集(support)的高維連續機率分布...
在此之後,狄利克雷過程作為貝葉斯決策理論中的先驗機率,被廣泛套用於非參數統計中。其後驗機率依然為狄利克雷過程。中文名 狄利克雷過程 外文名 Dirichlet Process...
在數學中,狄利克雷邊界條件,為常微分方程的“第一類邊界條件”,指定微分方程的解在邊界處的值。求出這樣的方程的解的問題被稱為狄利克雷問題。狄利克雷問題(...
狄利克雷原則簡介 編輯 狄利克雷原則即抽屜有時也被稱為鴿巢原理,它是德國數學家狄利克雷首先明確的提出來並用以證明一些數論中的問題,因此,也稱為狄利克雷原則...
狄利克雷空間論(theory of Dirichlet space)是受BLD函式組成的希爾伯特空間論的啟發,在狄利克雷空間上建立的一種公理位勢論。...
狄利克雷L函式,又稱對應於模q的特徵Ⅹ(n)的狄利克雷L函式。...... 又稱對應於模q的特徵Ⅹ(n)的狄利克雷L函式, 即函式,其中q≥1,Ⅹ(n)是模q的一個特...
狄利克雷區域是一類特殊區域。對於狄利克雷問題是可解的域D,稱為狄利克雷區域。...... 狄利克雷區域是一類特殊區域。對於狄利克雷問題是可解的域D,稱為狄利克...
狄利克雷形式亦稱狄氏型。狹義的狄氏型是指定義在如下希爾伯特空間 的一個稠密子空間D(E)上的、滿足一定條件的雙線性泛函E,即(Y,𝒥)是一個可測空間,μ是...
在數學中,費耶核(Fejér kernel)是用來表達對傅立葉級數進行切薩羅求和的結果的運運算元。費耶核是非負的恆等逼近,因此能解決狄利克雷核的局限。...
