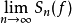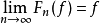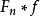費耶核

在數學中，費耶核（Fejér kernel）是用來表達對傅立葉級數進行切薩羅求和的結果的運運算元。費耶核是非負的恆等逼近，因此能解決狄利克雷核的局限。

基本介紹

• 中文名：費耶核
• 外文名：Fejér kernel
• 特點：是非負的恆等逼近
• 作用：解決狄利克雷核的局限

定義

Fejér核心定義為

是第k階Dirichlet核心。 它也可以封閉形式寫成

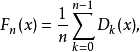
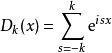
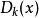
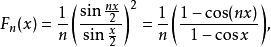
這個表達式的定義。

Fejér核心也可以表示為

。

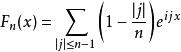
屬性

Fejér核心是一個積極的總結核心。 Fejér核心的一個重要特性是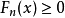，平均值為1。

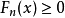
卷積

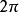卷積Fn是正數：對於時的它滿足

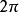
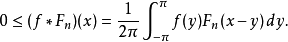
由於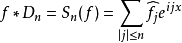，我們有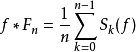，這是傅立葉級數的Cesàro求和。

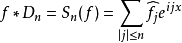
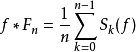
由卷積不等式

由於。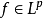

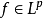
另外，如果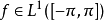，那么

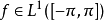
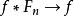
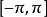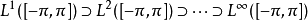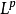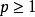由於是有限的，，因此結果適用於其他空格，也是如此。

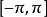
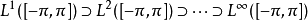
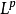
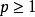
如果是連續的，則收斂是均勻的，產生Weierstrass定理的證明。

收斂是傅立葉係數的唯一性：如果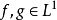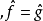，然後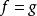a.e.這是通過寫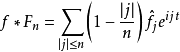它僅取決於傅立葉係數。

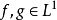
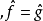
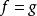
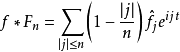
第二個結果是，如果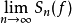存在a.e，那么 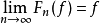a.e，因為Cesàro意味著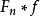會收斂到原始序列限制（如果存在）。