基本介紹
- 中文名:熱力學本構方程
- 外文名:Thermodynamic constitutive equation
建立的有效途徑
套用
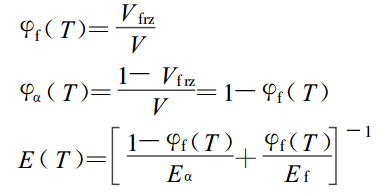
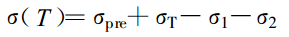
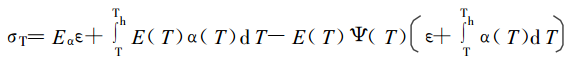
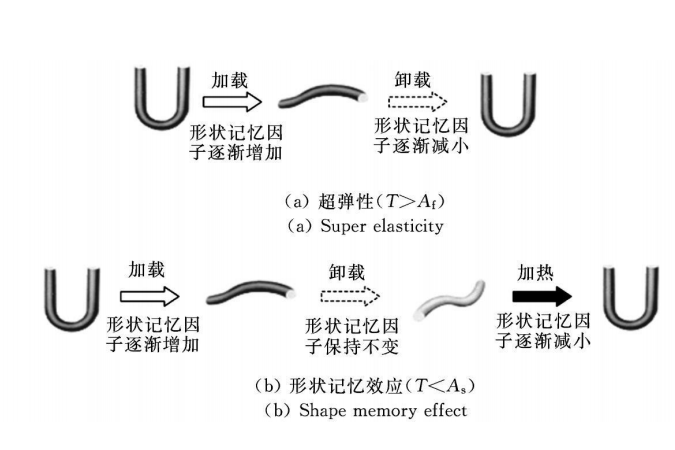
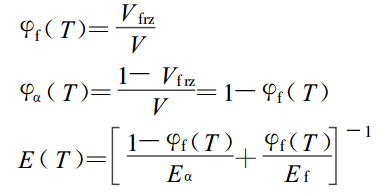
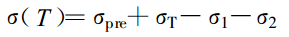
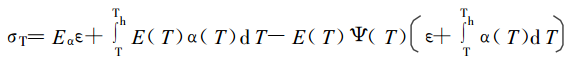
熱力學本構方程Helmholtz 自由能或者利用Gibbs自由能來實現的方程,主要套用於形狀記憶聚合物(SMP)的研究。基於不同預應變率下的熱力學實驗結果,通過考慮材料凍結/恢復過程中的時間延遲效應 、應力鬆弛效應以及熱...
本構方程(constitutive equation),反映物質巨觀性質的數學模型。又稱本構關係(constitutive relations) 。通常把應力和應變率,或應力張量與應變張量之間的函式關係稱為本構方程。又稱流變方程。描述特定連續介質運動學量、動力學量、熱力學...
更具體地,狀態方程是描述在一組給定的物理條件下物質的狀態的熱力學方程。它是一種本構方程,它提供與該物質相關聯的兩個或更多個狀態函式之間的數學關係,例如它的溫度,壓強,體積,或內能。狀態方程在描述流體、流體的混合物、固體...
本研究採用非平衡態熱力學方法,以飽和砂土為研究對象。首先,將飽和砂土簡化為固液兩相連續介質,構建其熱力學理論框架,得到砂土液化大變形行為的控制偏微分方程組;其次,探索合理的自由能和遷移係數模型,再現砂土液化大變形的基本規律,...
Φ的表達式對牛頓流體(見本構方程)是 。 (7)對於牛頓流體,用熱力學第一定律導出的能量方程為 (8)這是最一般流體的能量方程。自20世紀50年代以來,有人還考慮非牛頓流體或是無粘流體中的電磁力效應,也有人考慮摻在流體中的液...
發展反映工程岩體特點的岩體非線性力學的基本理論框架,研究建立多尺度反映熱、流、固、化多場並存及耦合的熱力學框架和基礎;研究發展反映岩體細觀結構非局部特性的本構描述方法和本構方程,為將介於連續與非連續介質之間的節理岩體納入連續...
式中Eₑ為自由電子的熱運動能量。相應地須考慮自由電子對金屬熱力學性質的影響。狀態方程 描述壓力p、體積V和溫度T之間函式關係的表達式。依據統計力學和熱力學,從固體的能量E可以推導出固體狀態方程:式中p為E對壓力的貢獻,稱為...
範圍更大的用於建立本構方程的定理和方法。以熱力學為基礎,基於多相孔隙介質理論對非飽和土進行研究是一個具有挑戰性的研究方向。圖書目錄 序 前言 上篇熱力學基礎理論 下篇理性土力學 參考文獻 附錄1符號表 附錄2代表性研究成果 ...
主要研究內容包括:(1)發展“連續基”水化模型,探討混凝土組分在水化和微結構形成過程中的作用機理;(2)基於“水化度”機制描述結構混凝土的早期特性,基於連續介質力學和熱力學基本定律構建結構混凝土的早期本構模型,並基於多尺度方法...
圖書目錄 封面 委員會 材料本構關係理論講義 內容簡介 第1章 張量和矩陣 第2章 運動和變形 第3章 動力學分析 第4章 變形熱力學 第5章 本構方程的一般原理 第6章 彈性 第7章 彈塑性 第8章 黏彈性 參考文獻 後記 索引 封底 ...
6.2.3熱力學相容性原理的限制216 6.2.4彈性流體流動的演化方程217 6.3可壓縮黏性流體220 6.3.1本構方程220 6.3.2構架無差異性(即客觀性)原理的限制220 6.3.3熱力學相容性原理的限制222 6.3.4實例:可壓縮線性黏性流體223...
7.1 多機制連續損傷模型的熱力學建模方案 7.1.1 多機制連續損傷模型的基本假設 7.1.2 狀態勢函式和模型本構方程 7.1.3 耗散型內部變數的本構發展方程 7.2 關於各向異性損傷狀態的討論 7.2.1 二階對稱損傷張量的引入 7.2.2...
2.3.4 熱力學方程 2.4 本構方程 2.4.1 牛頓型流體的本構方程 2.4.2 廣義牛頓型流體的本構方程 參考文獻 第3章 兩種結構的固-液態金屬流變學行為及觸變特性 3.1 枝晶結構固-液態金屬流變學 3.1.1 枝晶結構組織特徵 3...
[2]李鄭發,王正道,熊志遠,暢若妮, 形狀記憶聚合物熱力學本構方程, 高分子學報2009;1:23-27 [3]Y.H. Wang, Z.D. Wang, X.X. Zhao. Prediction of the fatigue life based on stiffness degradation concept, Advanced ...
本項目擬基於熱力學建立材料本構方程,結合鈦合金正交磨削試驗獲得熱力耦合本構模型,並藉助仿真技術預測工藝參數對溫度場變化的影響;通過SEM和能譜分析儀等儀器觀測固結金剛石磨粒的主要磨損形態(如擴散磨損、磨粒磨損和粘著磨損),分別對...
② 基於自由體積的概念,考慮了黏彈參數的時間-溫度-應力效應,通過狀態方程和本構方程推演,建立超音波特徵與聚合物比容及黏彈性的定量關係,從而建立方程參數求取方法。通過黏彈性和熱力學數據關聯,可分析工藝參數及材料組成的綜合效果。
4.2材料本構方程 4.2.1固體彈塑性本構方程 4.2.2流體本構方程 4.2.3粘彈性與粘塑性本構模型 4.3熱彈塑性分析 4.3.1熱彈性問題 4.3.2熱彈塑性問題 4.3.3熱變形與應力的簡化分析 4.4強瞬態熱力效應 4.4.1高能束加工...
