固體物理力學

物理力學的一個分支，是從固體的微觀結構理論出發，探求固體巨觀力學性質的學科。

物理力學的一個分支，是從固體的微觀結構理論出發，探求固體巨觀力學性質的學科。在固體物理力學中，固體被看成是原子、分子或離子在空間呈周期性有序排列而成的離散結構體。固體內部的原子、分子、離子和電子等微觀粒子之間的相互作用和它們的運動規律，可由量子力學和固體物理方法求出；然後用統計力學方法，通過理論計算或某些實驗,求得固體的巨觀力學性質,如固體的熱力學性質、狀態方程、彈性和塑性性質（見材料的力學性能）、本構關係以及強度等。

發展概況

19世紀，法國的A.布喇菲根據固體有序結構的特徵，提出了空間點陣學說,1912年,德國物理學家M.von勞厄用X射線衍射實驗予以證實。19世紀末，A.熊夫利等人把這一學說發展成為固體微觀幾何結構理論，為進一步研究固體微觀結構提供了依據。另一方面，一些學者根據實驗事實總結出若干個描述固體物質性質的經驗定律,例如，關於晶體比熱的杜隆-珀替定律和關於金屬傳導性質的維德曼-夫蘭茲定律等。在此基礎上,P.K.L.德魯德和H.A.洛倫茲建立了經典的金屬自由電子論。20世紀初，隨著量子理論的發展，人們對固體內部微觀粒子的相互作用和運動規律有了進一步了解並對這些經驗定律作出解釋。例如，A.愛因斯坦引進量子化概念研究點陣振動，A.索末菲把經典的金屬自由電子論發展成固體量子論，E.費密創立了量子統計理論。30年代，在量子力學的基礎上，逐步形成固體物理學，為後來固體物理力學的創立奠定了基礎。

40年代起，出現了核反應堆、核武器、火箭和飛彈等尖端技術，從而面臨著需要研究固體材料在高壓、高溫、高應變率等極端條件下的性質問題。例如，核爆炸可使周圍介質的壓力在約 10^-7秒時間內達到數百萬個大氣壓（1大氣壓等於101325帕）,這種條件在實驗室內很難模擬，因而不能再單純依靠實驗來直接測量固體材料在極端條件下的巨觀性質，而只能從固體微觀結構出發來間接計算。固體物理力學正是為滿足這種需要在50年代逐步發展起來的。

固體微觀結構的計算以及從微觀結構推算巨觀性質都包含大量複雜的數值計算。電子計算機的出現和發展，為進行這些計算創造了條件，促進了固體物理力學的發展。

理論基礎

固體的微觀幾何結構和微觀粒子間的相互作用勢以及點陣振動、缺陷等模型是固體物理力學的理論基礎。

固體微觀幾何結構

如果組成固體的原子、分子或離子在空間呈周期性重複排列，則固體的微觀幾何結構可描述成為許多相同的點子在空間的有序分布。這些點子稱為結點，其總體稱為空間點陣。通過點陣中的結點，可以作平行的直線族和平面族，於是空間點陣就成為一些格線，稱為晶格。具有一定晶格結構的固體稱為晶體。晶體中原子或分子分別保持一定的方向和距離而呈規則的幾何排列，這是晶體物質最基本的特點，是研究晶體內部各種微觀過程和巨觀性質的重要基礎。

相互作用勢

固體中的原子、分子或離子所以能結合成晶體，因為在它們之間存在著相互作用力。通常用原子或分子的相互作用勢描述這種作用力。確定相互作用勢有兩種基本方法：①用量子力學方法研究原子、分子的微觀結構，得出相互作用勢，所得的作用勢稱為第一原理相互作用勢。②假定相互作用勢具有某種典型形式，其中包含若干個待定參數，然後從實驗數據求出這些參數，按這種方法求出的作用勢稱為典型相互作用勢。前者無需實驗數據，但計算工作量相當大；後者計算量小，但需要若干組實驗數據。固體的結構與物性受到分子鍵合形式的決定性影響，因此，有關原子、分子的相互作用勢知識，是固體物理力學的重要理論基礎。

點陣振動

固體中的原子、分子或離子不停地在格點附近作熱振動。對於由N個原子構成的固體,這種熱振動可近似地用3N個簡正振動模式來描述，每個振動模式都是獨立的諧振動。實際上，點陣的熱振動並不是諧振動,否則就無法解釋熱膨脹現象。因此,在更為精確的理論中，需要引入非諧性修正。點陣振動可用點陣波（即原子振動波）描述，點陣波的量子稱為聲子。點陣振動頻率ν_i(i=1,2,…,3N)可由點陣結構和相互作用勢求出；根據頻譜，可直接得出晶體的熱容等巨觀性質參數。晶體的熱學性質、電學性質和光學性質以及晶體的相互作用等微觀過程，都涉及點陣振動，它是研究固體巨觀性質和微觀過程的基礎。

點陣缺陷

點陣結構完全規則的晶體，稱為理想晶體。實際上理想晶體並不存在，真實晶體總存在一些幾何結構的不規則性。這種對點陣結構規則性的破壞稱為缺陷，它們對晶體的性質有十分重要的影響。

按單一點陣排列而成的晶體稱為單晶體。大多數固體材料是由許多小單晶晶粒組成的，稱為多晶體。晶粒之間的交界面稱為晶粒間界，這是一種面缺陷。單晶體是各向異性的，多晶體中由於晶粒有各種空間取向，其巨觀性質往往表現為各向同性。位錯是晶體中的線缺陷，它是由於固體內原子的排列在一條線附近偏離了規則性而形成的，是決定金屬材料力學性質的一個重要因素。晶體的第三類缺陷是點缺陷，其原因是在點陣中出現了空位，或者是形成了間隙原子。在核輻射的輻照下固體中的點缺陷會增加，使巨觀力學性質改變。

固體物理力學對理想晶體的研究已有一定方法可循，對點缺陷和多晶體也有一些處理方法，但對關於位錯的一些問題，尚未徹底解決。固體的塑性和斷裂破壞與位錯密切相關。例如，由於位錯的存在，可使真實固體的強度比理想晶體的強度低三個數量級。因為對位錯的處理方法問題尚未完全解決，因而在固體本構方程和強度方面還沒有成熟的微觀理論，只能在亞微觀層次用半唯象方法處理。關於塑性的亞微觀理論稱為微力學。它涉及到位錯問題的微觀理論，是固體物理力學的難點所在。

研究課題

固體物理力學的主要研究課題是固體巨觀力學性質的計算，其中包括：

熱力學性質

根據統計力學，體系的各種熱力學函式都可以從它的配分函式導出，而配分函式又取決於體系的能量及其與溫度的關係。固體的能量可表示為：

E=E_c+E_t，

式中E_c與溫度無關，可由點陣結構和相互作用勢求出；E_t與溫度有關，若不考慮原子內部結構，它就是點陣熱振動的能量，與3N個振動頻率有關。求點陣熱振動的能量時,振動頻率有多種近似取法。愛因斯坦假定它們全都相等，並且互不相關；P.德拜則把點陣當作彈性連續介質來處理，其頻率上限ν_m可由自由度確定( ，g(v)為振動頻譜)或用溫度表示。德拜模型獲得廣泛採用,德拜溫度可由固體的彈性常數算出,也可以從比熱的實驗值求得。在更精確的理論中,可設頻率從ν到ν+dν範圍內分布有g(ν)dν個振動模式。g(ν)可由點陣結構和相互作用勢算出，也可以通過熱中子非彈性散射實驗得出。由於原子還有內部結構，因而計算配分函式時，有時還要考慮內部自由度的作用。

金屬中含有自由電子，金屬的能量可表示為：

E=E_c+E_t+E_e，

式中E_e為自由電子的熱運動能量。相應地須考慮自由電子對金屬熱力學性質的影響。

狀態方程 　描述壓力p、體積V和溫度T之間函式關係的表達式。依據統計力學和熱力學,從固體的能量E可以推導出固體狀態方程：

式中p_c為E_c對壓力的貢獻,稱為冷壓；p_t為E_t對壓力的貢獻，稱為熱壓。固體在壓力p的作用下，從微觀上看,由於點陣結構參數變化引起E_c變化；從巨觀上看，體積V發生變化。利用E_c和V之間的對應關係，可求出冷壓。熱壓可表示為：

p_t=ΓE_t/V_ζ，

式中Γ表示振動頻率ν與體積V之間的關係,稱為格呂內森係數。Γ可以從熱膨脹係數、壓縮係數和比熱求出,也可以從相互作用勢求出。

金屬中的自由電子熱運動能量 Ee對壓力也有貢獻，因此，金屬的狀態方程為：

p(V,T)=p_c(V)+p_t(V,T)+p_e(V,T)，

式中p_e稱為電子熱壓。

彈性性質

固體在應力的作用下發生變形。變形不大時，去掉應力之後變形可以完全恢復。這種變形稱為彈性變形。發生彈性變形後，固體的能量也要改變。從巨觀角度看，把固體視為連續介質，得出變形後的單位體積中勢能增加量為：

勢能增加量

式中η_ij為從巨觀角度描述變形的拉格朗日應變參數；c_ijkl稱為二級彈性常數；c_ijklmn稱為三級彈性常數。彈性常數給出固體的巨觀彈性性質。從微觀角度看，變形後點陣結構參數變化，引起E_c變化。單位體積固體中的E_c變化值就是勢能增加量w。 對比從巨觀與微觀兩種不同角度得到的w，即可求出固體的彈性常數。

本構方程

固體在較高的應力作用下，變形可超出彈性範圍，去掉應力之後形狀不能完全恢復。這時的應變ε可表示為：

ε=ε^e+ε^p，

式中ε^e為彈性應變；ε^p為塑性應變。彈性應變與應力間的關係用彈性常數表示，塑性應變與應力間的關係則很複雜，必須計及變形的速率。描述應力與應變間關係的表達式為本構關係。

塑性變形是位錯運動的結果。這時固體中原有的位錯中一部分發生運動，同時產生新的位錯。可動位錯運動時,其中一部分又會喪失掉可動性。在一維情況下,塑性應變率與位錯之間有奧羅萬關係：

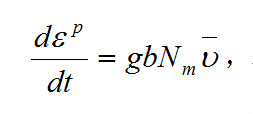
式中g為表示應力和應變方向的幾何因子；b為伯格斯矢量的大小;N_m為可動位錯密度；為平均位錯速度。伯格斯矢量由點陣結構確定。由奧羅萬關係導出本構方程，關鍵在於求出可動位錯密度N_m和平均位錯速度。當前還不能由固體微觀結構求出N_m和,只能通過分析動態高壓實驗數據，結合位錯動力學理論，唯象地定出它們與應力、應變之間的關係。在更為精確的理論中，本構方程內還要引入變形歷史以及溫度的影響。

強度

作用在固體上的應力足夠高時，可使固體斷裂而破壞。恰能使固體發生破壞時的臨界應力稱為固體的強度。固體在應力的作用下變形時，勢能將隨變形的加大而增大。如要加大變形，就必須施加更高的壓力。但當變形達到臨界值後，勢能反而會隨變形的進一步加大而減小，於是固體失去了穩定性，將自發地繼續變形，直到破壞。

由點陣結構和相互作用勢可以求出勢能，再計及點陣結構參數隨應力的變化關係後，即可得出固體的強度。如此算出的強度僅適用於理想晶體，稱為理想強度。真實固體中有缺陷，在較高的應力作用下會出於存在位錯而發生滑移，結果使強度遠小於理論強度。迄今還未能建立起定量計算真實固體強度的微觀理論。

參考書目

錢學森編La《物理力學講義》，科學出版社，北京，1962。

C.J. McMahon, Jr., ed., Microplasticity, Vol.2, Interscience, New York, 1968.

C. Caglioti, ed., Atomic Structure and Mechanical Properties of Metals, Proceedings of the. International School of Physics :Enrico Fermi” Course 61,North-Holland Pub. Co., Amsterdam, 1978.