無字證明

無字證明（英語：proof without words）是指僅用圖像而無需文字解釋就能不證自明的數學命題。由於其不證自明的特性，這種證明方式被認為比嚴格的數學證明更為優雅與有條理。[1]無字證明通常只是用圖像來說明一個證明中的特例，因而需要推廣才能構成完整的證明。[2]

簡介

（英語：proof without words）是指僅用圖像而無需文字解釋就能不證自明的數學命題。由於其不證自明的特性，這種證明方式被認為比嚴格的數學證明更為優雅與有條理。無字證明通常只是用圖像來說明一個證明中的特例，因而需要推廣才能構成完整的證明。

示例

奇數之和

從1至2n-1之間的所有奇數之和為平方數n的無字證明如右圖所示。第一個正方形由一個方塊組成，即1為首個平方數。之後增加3個白色方塊以組成第二個正方形，總共有4個方塊，即4為第二個平方數。之後再增加5個黑色方塊組成下一個平方數9，並以此類推。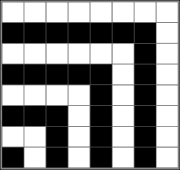

奇數之和

勾股定理

勾股定理可以由右邊第二張圖（出自《周髀算經》）進行證明。通過兩種不同的方法計算大的正方形的面積可以得到