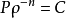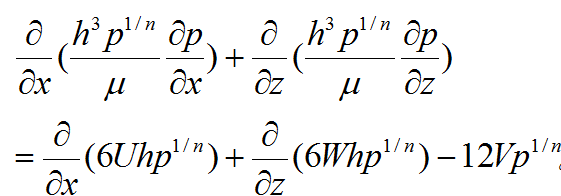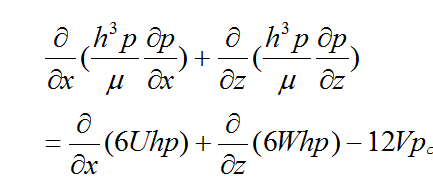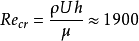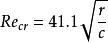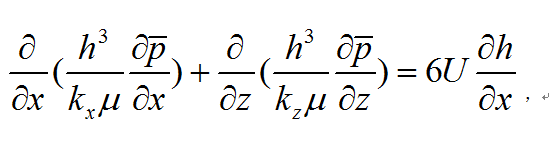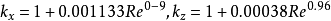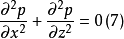簡介 設軸承和軸頸之間的狹縫中充滿粘性潤滑流體,當軸承以一定速度旋轉時產生巨大的壓差,軸頸被潤滑膜托起,形成偏心圓環,使軸承和軸頸避免直接接觸,起到減少摩擦阻力的潤滑作用。潤滑理論中通常假定:粘性流體作定常運動,而且處於層流狀態,潤滑膜的厚度比它的長度和寬度小得多;徹體力和慣性力忽略不計。因此潤滑理論屬於粘性流體小雷諾數流動的範圍。根據這些假定,可將流體力學基本方程組簡化為雷諾方程:
邊界條件為:
y=0 u=U v=V , w=W ,
y=h u=0 , v=0 , w=0,
圖1 潤滑膜示意圖 式中u、v、w分別為沿x、y、z坐標軸的流速分量;U、V、W為流速分量的邊界值;p為流體壓力;ρ為流體密度;μ為流體的動力粘性係數(見粘性);h為潤滑膜厚度(圖1)。此方程是潤滑理論的基本方程。式(1)是二價、二維、變係數、非齊次偏微分方程,一般難以求解,通常採用近似方法。
幾種主要類型的潤滑 油膜注滑 以油膜作注滑劑的潤滑。潤滑油一般是不可壓縮的,機器零件界面只有一個方向的運動 (u=U,υ=0,ω=0),所以式(1)可簡化為如下常用式
圖2 徑向軸承潤滑簡圖 圖2為徑向軸承的潤滑簡圖。圖中O為軸頸中心;O'為軸承中心;e為偏心距OO';r、R分別為軸頸半徑、軸承的內半徑;h為潤滑膜厚度;U為軸頸表面的線速度;θ為極角。對這類潤滑問題可將式(2)化為下式:
式中
。如果忽略z方向的壓力變化,且假定粘性係數不變,則式(2)可簡化為一維形式:
根據圖3,邊界條件為:x=0,p=0;x=l,p=0 (5) 。從式(4)、(5)可求得壓力分布p,單位寬度潤滑膜上所能承受的總支承力p和單位寬度動塊界面上的摩擦阻力F:
圖3 一維潤滑膜和壓力分布 式中符號的意義見圖3.。從圖3的壓力分布曲線可看出,最大壓力pmax 的位置不在滑塊中點,而在中點偏後處。|F|/|P|正比於小量h0 /l ,即變厚度薄層中的粘性流體運動能產生遠大於總摩阻的支撐力。在緩慢的變薄層粘性流動中產生高壓是潤滑型流動的顯著特點之一。
在上述計算中假設運動是一維的。事實上軸承在z方向的尺度是有限的,即有端泄效應。由於壓力在z方向上的減小,人們發現支承力較二維情形有顯著的減小。其次在計算中假設粘性係數是常數,這顯然是一種近似。由於摩擦生熱,潤滑油的溫度會升高,從而使油的粘度和支承力 曲線急劇下降。隨著高速和高溫(低粘度)的出現,慣性力變得可以和粘性力比擬,完全忽略慣性力的作法必須修正。可以採用逐次逼近法加以改進。計算表明,慣性修正一般不超過10%。 對於有z方向壓力變化的二維流動和兩偏心圓柱間的粘性流體運動須解式(2)和(3)。
氣膜潤滑 以空氣等氣體膜作潤滑劑的
潤滑 。這種潤滑,須考慮壓縮性影響。設氣體的壓力和密度滿足多方過程方程:
式中n 為多方指數。將上式代入(1)式,即得氣膜潤滑的雷諾方程:
通常氣膜潤滑可看作等溫過程,即n=1,於是得到:
即使在最簡單情況下,氣膜潤滑的雷諾方程也是複雜的,一般須用數值方法求解。
上述雷諾方程的各種形式只適用於低速區。如果慣性力和粘性力為同一數量級,由於運動微分方程中包含非線性項,就難以求出此方程的精確解。如果慣性力在總的流體動力中的作用較小,可用疊代法、平均慣性法、級數展開法等近似法求解。
對於剪下流動,實驗求得的層流轉變為湍流的臨界雷諾數
,對於壓力流動,臨界雷諾數一般取
Re cr =2000。實際上,在軸承潤滑中,由於兩種形式的流動同時存在,穩定性更差,因此,在一般軸承設計中取
Re cr =1000。對於徑向軸承,則取
。
流動狀態轉變為
湍流 後,必須根據湍流理論求解。湍流潤滑的研究開始較晚。現有湍流潤滑的計算方法一般屬於“0”方程模式和“1”方程模式。對於不可壓縮準定常二維湍流潤滑,基本方程為:
式中pˉ為平均壓力,kx kz 為湍端流係數。湍流潤滑方程形式上類似於上述雷諾方程。在工程計算中,由於所取的湍流模式不同,湍流係數也不同。如果選用建立在壁面律基礎上的湍流模式,則取
彈性流體動力潤滑 具有變粘性係數潤滑膜和彈性變形接觸面的潤滑。例如,齒輪嚙合時的潤滑以及球軸承的球體與內、外圈之間的潤滑。它們的共同特點是載荷作用在微小的接觸面積上,形成高壓區,從而使潤滑劑的粘性係數發生變化,接觸面發生彈性變形。這類彈性流體潤滑問題的研究,歸結為聯立求解潤滑方程、彈性變形方程和粘性-壓力方程。如果等溫條件不再有效,還要考慮潤滑的能量方程和熱傳導方程。此外,要套用氣穴邊界條件,計算非常複雜。工程計算中常用的是簡化後的半經驗半理論的公式。
流體靜力潤滑 潤滑膜兩界面無相對切向運動的潤滑。上述基本潤滑方程均屬流體動力潤滑範圍。對於這類潤滑問題,潤滑膜建立的必要條件是兩界面必須有相對的切向運動,膜厚必須收斂。但是,對於流體靜力潤滑問題,由於潤滑膜的建立僅依賴於壓差,因此只需要一個邊界上的壓力高於另一邊界上的壓力。對於二維靜力潤滑問題,雷諾方程可簡化為拉普拉斯方程:
這類潤滑問題的邊界條件也比較簡單(例如空穴現象很少發生),因此,對於常用的任何形狀的潤滑膜,一般都可求得數值解。
除以上幾種類型的潤滑外,在核發反應堆和核動力渦輪發電機等高溫和液態金屬的工作環境中,有人研究採用磁流體潤滑,以便通過外加電磁場來提高液態金屬潤滑滑膜的承載能力。因導電流體通過磁場時會感生電流,電流和磁場相互作用產生洛倫茲力,這個力的方向與粘性力的方向一致,從而提高承載能力。
參考文獻 詞條作者:郭本鐵 應玉燕.《中國大百科全書》74卷(第一版)力學 詞條:流體力學中國大百科全書出版社 ,1987 :413-414頁
O.平克斯、B. 斯德因李希特著,西安交通大學軸承研究小組譯:《流體動力潤滑理論》,機構工業出版社,北京,1980。(O. Pin-kus and B. Sternlicht, Theory of Hydrodynamic Lubrica-tion, McGraw-Hill, New York, 1961.)
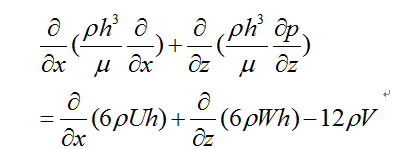
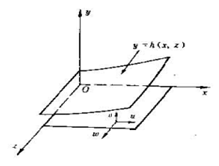 圖1 潤滑膜示意圖
圖1 潤滑膜示意圖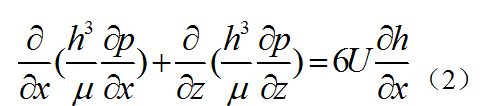
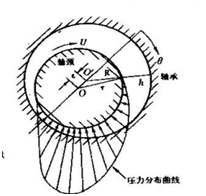 圖2 徑向軸承潤滑簡圖
圖2 徑向軸承潤滑簡圖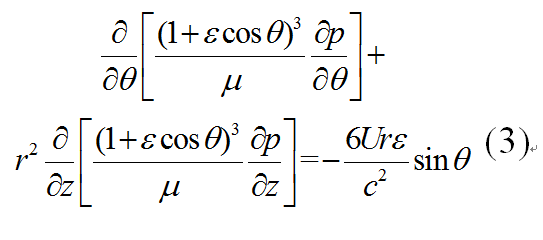
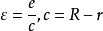
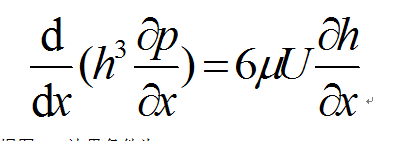
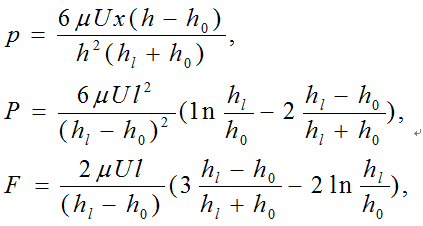
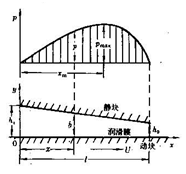 圖3 一維潤滑膜和壓力分布
圖3 一維潤滑膜和壓力分布