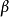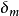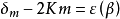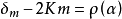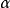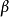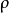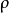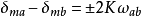簡介
材料在屈服時,試樣表面出現的線紋稱為滑移線。
 滑移線
滑移線滑移線理論是二十世紀20年代至40年代間,人們對
金屬塑性變形過程中,光滑試樣表面出現“
滑移帶”現象經過力學分析,而逐步形成的一種圖形繪製與
數值計算相結合的求解平麵塑性流動問題變形力學問題的理論方法。這裡所謂“
滑移線”是一個
純力學概念,它是塑性變形區內,最大剪下應力)等於材料屈服切應力(k)的軌跡線。
滑移線與滑移線場
變形體處於塑性平面應變狀態時,在塑性流動平面上(塑性區)各點的應力狀態均滿足屈服準則,而且過任一點P都存在兩個相互正交的第一、第二剪下方向。一般來說,這兩個方向將隨P點的位置而變化。當屍點的位置沿最大切應力方向連續變化時,則得兩條相互正交的最大切應力方向的軌跡線,即稱為滑移線。滑移線上任一點的切線方向即為該點的最大切應力方向。將P點沿第一剪下方向所得的滑移線稱為
線,沿第二剪下方向所得的滑移線稱為
線。由於過塑性區內任一點均可引出兩條相互正交的滑移線,從而可構成滑移線網路,它們布滿於塑性區,形成滑移線場,如圖。

研究發展
在岩土穩定性分析的工程實踐中,幾乎沒有例外地都採用極限平衡法。對於邊坡一般採用條分法,條分法是1916年由瑞典人彼德萊提出的,後經過費倫紐斯、泰勒等人的不斷改進,計算方法已日趨完善,其基本出發點都是一樣的,就是假定岩土是理想塑性材料,把土條作為一個剛體,按極限平衡的原則進行受力分析,完全不考慮土體本身的應力應變關係。各種方法最大的不同之處僅僅在於對相鄰岩土條之間的內力作不同假定,也就是如何增加已知條件使超靜定問題變成靜定問題。這些假定的物理意義不一樣,所能滿足的平衡條件也不相同,分析結果也就相差較大。
傳統的滑移線理論,只適合於平面應變或軸對稱問題,該理論比起極限平衡理論更嚴密一些,是岩土材料的一個重要理論。通過研究現有的平面應變滑移線理論,我們可以發現,現在的理論均是基於剛塑體的Prandl -Reuss假設,假定岩土中所有點均達到破壞狀態,不考慮岩土的變形過程,認為岩土是剛塑性材料,破壞以後可以無限地流動,只對岩土最後破壞狀態進行研究,由靜力平衡微分方程和強度準則聯合求解岩土應力及特徵線。這方面的專著和論文也不少,說明該理論在岩土界很受重視,但除個別情況外,一般不可能通過特徵線得出理論解,大部分問題只能用差分法求解。而關鍵的問題是還沒有象有限元法這樣通用的差分法程式,只能針對具體問題編制相應程式。所以除進行科學研究外,很少有人會用差分法按傳統的滑移線理論去求解實際岩土問題。
在微型計算機飛速發展的今天,有限元方法的通用性和成熟性,邊坡的穩定性問題應該轉向用有限元方法分析,彈塑性有限元方法不僅考慮了岩土的靜力平衡條件,而且考慮了岩土的應力應變關係。儘管有人會說岩土材料的應力應變關係複雜,其力學參數很難準確地獲得,這對分析結果會產生很大的影響。但彈塑性有限元分析結果,至少能保證岩土內各點滿足靜力平衡和破壞條件,而條分法不能嚴格地滿足靜力平衡和破壞條件。利用有限元分析邊坡穩定性,能夠揭示出邊坡可能受損或破壞的部位、應力及應變的分布和大小,確實具有常規方法不可達到的優點。因此,彈塑性有限元分析結果肯定會更有說服力。
但關鍵是如何利用有限元分析結果得出邊坡穩定性指標,用一個什麼樣指標來評判邊坡穩定性;邊坡破壞時,如何用有限元結果確定滑移面或潛在滑移面,暫無好的解決辦法。因此,張國祥等針對以上問題進行研究,建立一套比傳統滑移線(特徵線)理論更嚴密、更普遍的潛在滑移線理論,根據潛在滑移線理論,用有限元分析結果建立一套確定邊坡潛在滑移面和評判邊坡穩定性的新方法,並編制了通用彈塑性有限元程式、前後處理程式和潛在滑移線求解程式。
滑移線的主要特性
對於理想剛塑性材料處於塑性平面應變狀態’下,塑性區內各點的應力狀態不同其實質只是平均應力
不同,而各點處的最大切應力K為材料常數。
沿滑移線上各點的平均應力的變化規律由著名的亨蓋應力方程來描述,即
亨蓋應力方程是滑移線場理論中很重要的公式,滑移線場的若干特性可直接或間接地由它導出。
當沿
族(或
族)中的同一條滑移線移動時,
(或
)為常數。只有當一條滑移線轉到同族的另一條滑移線時,
(或
)值才改變。
在任一族中的任意一條滑移線上任取兩點,則可導得
由式可得出以下幾點結論:
(1)若滑移線場已經確定,且已知一條滑移線上任一點的平均應力,則可確定該滑移線場中各點的應力狀態。
(2)若滑移線為直線,則此直線上各點的應力狀態相同。
(3)如果在滑移線場的某一區域內,兩族滑移線皆為直線,則此區域內各點的應力狀態相同,稱為均勻應力場。
 滑移線
滑移線