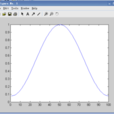
海明窗也是餘弦窗的一種,又稱改進的升餘弦窗。海明窗與漢寧窗都是餘弦窗,只是加權係數不同。海明窗加權的係數能使旁瓣達到更小。分析表明,海明窗的第一旁瓣衰減為一42dB.海明窗的頻譜也是由3個矩形時窗的頻譜合成,但其旁瓣衰減速度為20dB/(10oct),這比漢寧窗衰減速度慢。
基本介紹
- 中文名:海明窗
- 外文名:Hamming
- 用途:FIR濾波器
- :
簡介,相關介紹,
簡介
語音信號一般在10ms到30ms之間,我們可以把它看成是平穩的。為了處理語音信號,我們要對語音信號進行加窗,也就是一次僅處理窗中的數據。因為實際的語音信號是很長的,我們不能也不必對非常長的數據進行一次性處理。明智的解決辦法就是每次取一段數據,進行分析,然後再取下一段數據,再進行分析。
怎么僅取一段數據呢?一種方式就是構造一個函式。這個函式在某一區間有非零值,而在其餘區間皆為0.漢明窗就是這樣的一種函式。它主要部分的形狀像sin(x)在0到pi區間的形狀,而其餘部分都是0,這樣的函式乘上其他任何一個函式f,f只有一部分有非零值。
為什麼海明窗這樣取呢?因為之後我們會對海明窗中的數據進行FFT,它假設一個窗內的信號是代表一個周期的信號。(也就是說窗的左端和右端應該大致能連在一起)而通常一小段音頻數據沒有明顯的周期性,加上漢明窗後,數據形狀就有點周期的感覺了。
因為加上海明窗,只有中間的數據體現出來了,兩邊的數據信息丟失了,所以等會移窗的時候,只會移1/3或1/2窗,這樣被前一幀或二幀丟失的數據又重新得到了體現。
簡單的說海明窗就是個函式,它的形狀像窗,所以類似的函式都叫做窗函式。
函式形式為:
W(n,α ) = (1 -α ) - α cos(2*PI*n/(N-1)),0≦n≦N-1, 一般情況下,α取0.46 。
相關介紹
海明窗也是餘弦窗的一種,又稱改進的升餘弦窗。海明窗與漢寧窗(Hanning)都是餘弦窗,只是加權係數不同。海明窗加權的係數能使旁瓣達到更小。分析表明,海明窗的第一旁瓣衰減為一42dB.海明窗的頻譜也是由3個矩形時窗的頻譜合成,但其旁瓣衰減速度為20dB/(10oct),這比漢寧窗衰減速度慢。