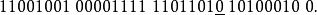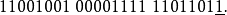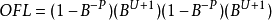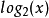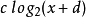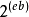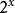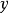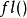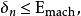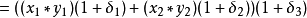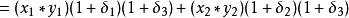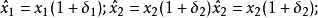浮點簡單講就是實數的意思，浮點數在計算機中用以近似表示任意某個實數。具體的說，這個實數由一個整數或定點數（即尾數）乘以某個基數（計算機中通常是2）的整數次冪得到，這種表示方法類似於基數為10的科學記數法。浮點精細度就是實數的精細程度。
基本介紹
- 中文名：浮點精細度
- 外文名：Floating point precision
- 套用領域：計算機
- 本質：實數的精細程度
- 換算方式：二進制
- 學科：數理科學
浮點數字,浮點數範圍,IEEE 754：現代計算機中的浮點,內部表示,機器精度和後向誤差分析,
浮點數字
一個數字表示指定編碼數字，通常為一個數字串的某種方式。
有幾種數字字元串可以代表數字的機制。在通用數學符號中，數字串可以是任意長度的，並且小數點的位置通過在那裡放置明確的“點”字元（點或逗號）來指示。如果沒有指定小數點，那么字元串隱含地表示一個整數，並且未指定的小數點將離開字元串的右端，在最低有效數字的旁邊。在定點系統中，字元串中的位置是為小數點指定的。所以一個定點方案可能是使用一個小數點位於中間的8位十進制數字串，其中“00012345”代表0001.2345。
在科學記數法中，給定的數字是以10的冪來縮放的，以便它位於一定的範圍內，通常在1到10之間，小數點緊跟在第一個數字之後。比例因子作為十的冪，然後在數字的末尾單獨指示。例如，木星的月亮Io的軌道周期為152,853.5047秒，這個值將以標準形式的科學記數法表示為1.528535047×10秒。
浮點表示在概念上與科學記數法類似。從邏輯上講，浮點數包括：
- 有符號的整數指數（也稱為特徵或比例），用於修改數字的大小。
為了導出浮點數的值時，有效數由乘以基升高到的功率指數，相當於由等於的指數對值的號碼的地方移位從它隱含位置小數點如果指數是正值，則表示右邊，如果指數是負值，則表示為左邊。
以base-10（熟悉的十進制符號）為例，編號為152,853.5047的精度為十位十進制數字，表示為有效數字1,528,535,047以及5作為指數。為了確定實際值，在有效數字的第一位之後放置一個小數點，結果乘以10得到1.528535047×10或152,853.5047。在存儲這樣一個數字時，基礎（10）不需要被存儲，因為它對於整個支持的數字範圍是相同的，因此可以推斷出來。
象徵性地，這個最終值是：
其中s是有效數字（忽略任何隱含的小數點），p是精度（有效數字中的位數），b是基數（在我們的例子中，這是數字10），e是指數。
浮點數是一個有理數，因為它可以表示為一個整數除以另一個;例如1.45×10是（145/100）×1000或145,000/ 100。基數決定了可以表示的分數;例如，1/5不能完全表示為使用二進制基數的浮點數，但1/5可以精確地用小數（0.2或2×10）表示。然而，1/3不能用二進制（0.010101 ...）或十進制（0.333 ...）來表示，但是在基數3中，它是微不足道的（0.1或1×3）。發生無限擴展的場合取決於基礎及其主要因素，如位置標記文章中所述。
有效數（包括其符號）和指數存儲在計算機中的方式取決於實現。常見的IEEE格式在後面和其他地方詳細描述，但作為例子，在二進制單精度（32位）浮點表示中，{\ displaystyle p = 24}，所以有效位是一個24位的字元串。例如，數字π的前33位是：
在這個二進制擴展中，讓我們表示從0（最左邊的位或最高有效位）到32（最右邊的位）的位置。24位有效位將在位置23停止，如上面帶下劃線的位0所示。下一位，在位置24，被稱為圓位或舍位位。它用於將33位近似值四捨五入為最接近的24位數（對於中途值有特定的規則，這裡不是這種情況）。在這個例子中，該位是1，被加到由最左邊的24位形成的整數上，產生：
當這是使用IEEE 754編碼存儲在存儲器中，這成為有效數小號。假定有效位在最左邊的位右邊有一個二進制點。
可以要求非零數字的有效位的最高有效位數不為零（除非相應的指數小於最小數字）。這個過程被稱為規範化。對於二進制格式（僅使用數字0和1），此非零數字必須為1。因此，它不需要在記憶體中表示;允許格式有更多的精度。這個規則被不同地稱為前導位約定，隱式位約定或隱藏位約定。
浮點數範圍
浮點數由兩個定點組件組成，其範圍完全取決於表示中的位數或位數。雖然分量線性取決於它們的範圍，但是浮點範圍線性地依賴於指數分量範圍內的顯著範圍和指數函式，這在數量上顯著地增大了範圍。
在典型的計算機系統中，“雙精度”（64位）二進制浮點數的係數為53位（其中一個隱含），指數為11位，符號位為1。由於指數的範圍是[-1022,1023]，而308大約是log10（2），所以此格式的正浮點數的範圍大約在10到10。格式的完整範圍從大約-10到+10（見IEEE 754）。
系統（B，P，L，U）中的歸一化浮點數的數量
- B是系統的基礎，
- P是系統對P數的精度，
- L是系統中可表示的最小指數，
- 和ü是在系統中使用的最大的指數）
是 
有一個最小的正歸一化浮點數，下溢級別
其中以1為前導數字，0為有效數字的剩餘數字，以及指數的最小可能值。
有一個最大的浮點數，溢出級別
其中B-1是有效數字的每個數字的值，並且是指數的最大可能值。
另外，在-UFL和UFL之間還有可表示的值。即，正數和負數的零，以及非規格化的數字。
IEEE 754：現代計算機中的浮點
在IEEE標準化二進制浮點數字的計算機表示在IEEE 754在1985年（又名IEC 60559）這個第一標準之後，幾乎所有現代機器。2008年進行了修訂。IBM大型機除支持IEEE 754二進制格式外，還支持IBM自己的十六進制浮點格式和IEEE 754-2008十進制浮點數。在克雷T90系列有一個IEEE版本，但SV1仍然使用的Cray浮點格式。
該標準提供了許多密切相關的格式，只有少數細節不同。其中五種稱為基本格式，另一種稱為擴展格式;其中三個特別廣泛地用於計算機硬體和語言：
- 單精度，通常用於表示C語言系列中的“float”類型（雖然這不能保證）。這是一個二進制格式，占用32位（4位元組），其有效位數的精度為24位（約7位十進制數字）。
- 雙精度，通常用來表示C語言系列中的“double”類型（雖然不能保證）。這是一個占用64位（8位元組）的二進制格式，其有效位數的精度為53位（約16位十進制數字）。
- 雙擴展，也稱為“擴展精度”格式。這是一個二進制格式，占用至少79位（如果不使用隱藏/隱式位規則，則為80位），其有效位數的精度至少為64位（19位十進制數）。x86體系結構提供了滿足最低要求（64位精度，15位指數，從而適應80位）的格式。通常在這樣的處理器上，這種格式可以在C語言系列（C99和C11）中使用“long double”標準“IEC 60559浮點運算擴展 - 附屬檔案F”推薦將80位擴展格式提供為“長雙”（如果可用））。在其他處理器上，如果任何形式的擴展精度不可用，“long double”可能是“double”的同義詞，或者可能代表更大的格式，如四倍精度。
增加浮點表示的精度通常會減少由中間計算引起的累積捨入誤差量。不太常見的IEEE格式包括：
- 四倍精度（binary128）。這是一個占用128位（16位元組）的二進制格式，其有效位數的精度為113位（約34位）。
- 雙精度（decimal64）和四精度（decimal128）十進制浮點格式。這些格式與單精度（decimal32）格式一起，用於正確執行小數四捨五入。
任何絕對值小於2整數都可以用單精度格式精確表示，絕對值小於2任何整數都可以用雙精度格式精確表示。而且，可以表示這樣一個數字的2倍的廣泛的權力。這些屬性有時用於純粹的整數數據，在具有雙精度浮點數但只有32位整數的平台上得到53位整數。
該標準指定了一些特殊的值，它們的表示形式：正無窮（+∞），負無窮（-∞），與普通（“正”）零不同的負零（-0）和“不是數值”NaNs）。
按照IEEE標準定義的浮點數比較與通常的整數比較有點不同。負的和正的零比較相等，每個NaN比較不等於每個值，包括它本身。除了NaN，所有的值都嚴格小於+∞，嚴格大於-∞。有限的浮點數以與它們的值相同的方式排列（在實數集合中）。
內部表示
浮點數通常從左到右被打包成一個計算機數據，作為符號位，指數欄位和有效數或尾數。對於具有現存硬體實現的IEEE 754二進制格式（基本和擴展），它們分配如下：
| 類型 | 標誌 | 指數 | 重要的領域 | 總比特數 | 指數偏差 | 比特精度 | 小數位數 |
|---|---|---|---|---|---|---|---|
一半（IEEE 754-2008） | 1 | 五 | 10 | 16 | 15 | 11 | 〜3.3 |
1 | 8 | 23 | 32 | 127 | 24 | 〜7.2 | |
1 | 11 | 52 | 64 | 1023 | 53 | 〜15.9 | |
x86擴展精度 | 1 | 15 | 64 | 80 | 16383 | 64 | 〜19.2 |
1 | 15 | 112 | 128 | 16383 | 113 | 〜34.0 |
指數可以是正數，也可以是負數，二進制格式的數據存儲為一個無符號數字，加上一個固定的“偏差”。該欄位中所有0的值保留為零和低於正常的數字;全1的值保留給無窮大和NaN。歸一化數字的指數範圍為[-126,127]為單精度，[-1022,1023]為雙精度，或[-16382,16383]為四。規範化的數字不包括低於正常值，零，無窮和NaN。
在IEEE二進制交換格式中，標準化的有效位的前1位實際上並不存儲在計算機數據中。它被稱為“隱藏”或“隱含”位。正因為如此，單精度格式實際上有24位精度的有效位數，雙精度格式有53位，四位有113位精度。
例如，上面顯示的是π，四捨五入到24位的精度，具有：
- sign = 0;e= 1;s= 110010010000111111011011（含隱藏位）
指數偏差（127）和指數（1）的總和為128，所以這是以單精度格式表示為
- 0 10000000 10010010000111111011011（不含隱藏位）= 40490FDB為十六進制數。
分段線性逼近指數和對數
如果我們繪製一個點陣圖模式的浮點值（x軸是位模式，被認為是整數，y軸是浮點數的值;假設是正的），可以得到移位的分段線性近似值基數為2的縮放指數函式，
（因此實際上 
）。相反，給定一個實數，如果採用浮點表示法並將其視為一個整數，則可以得到移位和縮放的基2對數的分段線性近似，
（因此實際上
），如右圖所示。
這種解釋對於顯示浮點數的值隨著表示的變化是有用的，並且允許通過整數運算和位移對浮點運算進行某些有效的近似。例如，將float重新解釋為一個整數，取其負數（或者從一個固定的數字中減去，由於偏差和隱含的1），然後重新解釋為一個浮點數，得到倒數。明顯地，忽略有效數，取倒數只是取（無偏）指數的加法倒數，因為倒數的指數是原指數的負數。（因此，實際上從偏差的兩倍中減去指數，這對應於非偏置，取負，然後偏置。）對於有效數，近似1倒數近似為線性：
（因為衍生物是 
;這是泰勒級數的第一項），因此對於有效數據，取負數（或者從固定數減去處理隱含1）近似取倒數。
更重要的是，位移允許計算平方（左移1）或取平方根（右移1）。這導致近似計算平方根;結合之前的逆向技術，這允許在20世紀80年代末和90年代在圖形處理中重要的快速平方根計算。這可以在其他一些套用中被利用，例如數字聲音處理中的音量增加。
具體地說，每次指數遞增時，數值加倍（因此按指數增長），而每次有效數遞增（對於給定的指數），數值增加
（因此線性增長，斜率等於指數的實際值（無偏））。即使對於給定指數的最後一步，其中有效數溢出到指數中：對於隱含1，1.11 ... 1之後的數是2.0（不管指數），即指數的增量：
- （0 ... 001）0 ... 0到（0 ... 001）1 ... 1，（0 ... 010）0 ... 0是相同的步長（線性）
因此，作為一個圖形，它是線性的（對於一個給定的指數，隨著有效數字的增長）連線兩個均勻間隔的冪（當有效數為0時），每個線性片具有前一個斜率的兩倍：它大約是一個縮放並轉移指數 
。每件作品採用相同的水平空間，但最後的兩倍是垂直空間。由於指數是凸起的，因此通過有效數為0的點，該值總是大於或等於實際（移位和縮放的）指數曲線;通過略有不同的轉變，人們可以更接近於指數，有時高估，有時低估。相反，將一個浮點數解釋為一個整數給出了一個近似的移位和縮放對數，每個塊都有最後一個斜率的一半，取相同的垂直空間，但水平空間的兩倍。由於對數是向下凸的，所以近似值總是較小比對應的對數曲線;再次，一個不同的尺度和偏移選擇（如右上方）產生了一個更接近的近似值。
機器精度和後向誤差分析
機器精度是表征浮點系統精度的量，用於浮點算法的後向錯誤分析。它也被稱為單位捨入或機器epsilon。通常表示為Emach，其值取決於所使用的特定捨入。
四捨五入為零，
而捨入到最近，
這很重要，因為它限制了在浮點系統的標準化範圍內表示任何非零實數x的相對誤差：
向後的誤差分析，其理論由James H. Wilkinson開發和推廣，可以用來確定實現數值函式的算法在數值上是穩定的。基本的方法是表明雖然計算結果由於捨入誤差而不會是完全正確的，但對於附近有輕微干擾的輸入數據的問題來說，這是確切的解決方案。如果所需的擾動很小，則按照輸入數據中的不確定性的順序，那么結果在某種意義上與數據“應得”一樣準確。算法被定義為後向穩定。穩定性是對給定數值過程的捨入誤差敏感度的度量;相比之下，條件編號對於一個給定的問題的函式表示該函式對其輸入中的小擾動的內在敏感性，並且與用於解決該問題的實現無關。
作為一個簡單的例子，考慮一個簡單的表達式給出（長度二）向量的內積 
和 
， 然後
其中
指示正確捨入的浮點運算
其中 
， 從上面
其中
其中
這是兩個微擾（Emach的數量級）輸入數據的總和，所以是後向穩定的。數值線性代數中更實際的例子見Higham 2002和下面的其他參考文獻。
