流體平衡方程表達了處於靜止(或相對靜止)狀態的流體中任一點上壓強與作用於流體的質量力之間的普遍關係。
基本介紹
- 中文名:流體平衡方程
- 別稱:歐拉平衡方程
- 提出者:歐拉
- 提出時間:是1755
- 適用領域範圍:流體力學,靜力學
方程式
推導過程
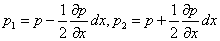

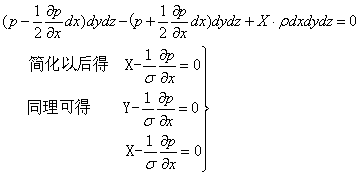
流體平衡方程表達了處於靜止(或相對靜止)狀態的流體中任一點上壓強與作用於流體的質量力之間的普遍關係。
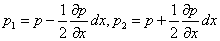

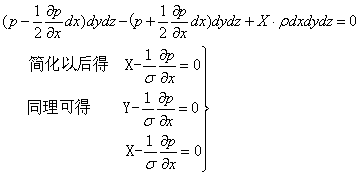
流體平衡方程表達了處於靜止(或相對靜止)狀態的流體中任一點上壓強與作用於流體的質量力之間的普遍關係。...
流體靜壓力流體平衡微分方程 在靜止流體中取邊長為dx,dy,dz的微元六面體,如下圖2所示,微小平行六面體各邊長度dx、dy、dz,各與相應的坐標軸平行。現在來分析這...
在絕對靜止的大氣中,表示空氣微團的浮力與重力平衡關係的方程。...... 在絕對靜止的大氣中,表示空氣微團的浮力與重力平衡關係的方程。中文名稱 流體靜力方程 英文...
2 2流體平衡微分方程142 2 1流體平衡微分方程142 2 2等壓面方程152 3流體靜力學基本方程162 3 1重力作用下的流體平衡方程16...
1.4 作用在流體上的力1.5 流體的主要物理性質習題第2章 流體靜力學2.1 流體靜壓強及其特性2.2 流體平衡微分方程式2.3 重力場中流體的平衡...
1.5 作用於流體上的力思考題習題1第二章 流體靜力學2.1 靜止流體中應力的特性2.2 流體平衡微分方程2.3 重力作月T流體靜壓強的分布...
第六節 液體的相對平衡習題第三章 一元流體動力學基礎第一節 恆定流動與非恆定流動第二節 流線和跡線第三節 一元流動模型第四節 連續性方程...
2?2流體平衡微分方程2?2?1流體平衡微分方程2?2?2平衡微分方程的全微分式2?2?3等壓面2?3重力場中流體靜壓強的分布規律2?3?1液體靜力學基本方程...
1.2 流體質點和連續介質模型 1.3 作用在流體上的力 1.4 流體的主要物理性質 第2章 流體靜力學 2.1 流體靜壓強的特性 2.2 流體平衡微分方程 2.3...
靜止流體的平衡方程、靜止流體對物體表面的作用力及力矩、流體的相對平衡流體運動學講述流體運動的主要描述方法、跡線與流線、連續方程、流函式和勢函式理想流體動力學...
7.3.1靜止流體內應力 7.3.2靜止流體平衡方程 7.3.3重力場中的靜流體 7.3.4液體表面張力 7.3.5用流體靜力學方法討論潮汐高度 7.4流體的定常流動 7.4...
1 流體力學基礎1.1 流體力學基本概念1.1.1 流體的主要物理性質1.1.2 流體靜壓與靜壓頭1.1.3 靜止流體平衡方程1.2 流體運動若干基本概念...
3.4 固體和流體平衡方程“弱形式”的虛功原理 3.5 針對變數的部分離散 3.6 收斂性 3.7 什麼是變分原理 3.8 “自然”變分原理以及與控制微分方程的關係...
3.4固體和流體平衡方程“弱形式”的虛功原理3.5針對變數的部分離散3.6收斂性3.7什麼是變分原理3.8“自然”變分原理以及與控制微分方程的關係...
1.2.5 孔隙流體平衡方程 1.2.6 滲流連續方程 1.2.7 總控制方程 1.3 岩土工程基本分析方法 1.3.1 總應力分析法及其控制方程 1.3.2 有效[...
2.4 流體微團運動分析本章小結習題第3章 動量傳輸的基本方程3.1 質量守恆定律與流體流動的連續性方程3.2 黏性流體動量平衡方程(納維-斯托克斯方程)...
