基本介紹
- 中文名:波動率微笑
- 外文名:Volatility smiles
- 期權隱含波動:(implied volatility)
- 行權價格:strike price
- 價內期權:in the money
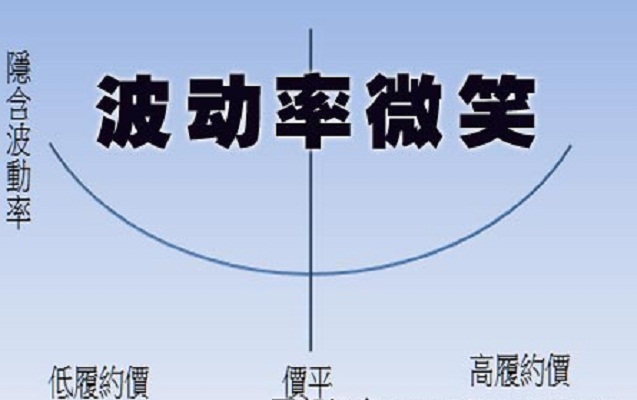
波動率微笑(Volatility smiles)指期權隱含波動率(implied volatility)與行權價格(strike price)之間的關係。波動率微笑現象是期權市場中常見的現象,對指導期權投資具有...
期權微笑又稱為波動率微笑(volatility smiles),是形容期權隱含波動率(implied volatility)與行權價格(strike price)之間關係的曲線。...
對於新的研究領域,包括隱含波動率曲線(implied volatility curves)、波動率微笑(volatility smile)和交易狀態指標(TRI),本文都做了闡述。作者還給出一系列示例,說明...
恐慌指數 = 芝加哥期權交易所VIX指數(CBOE Volatility Index)VIX(Volatility Index)波動率指數...
18.1為什麼波動率微笑對看漲期權與看跌期權是一樣的38918.2外匯期權39018.3股票期權39318.4其他刻畫波動率微笑的方法39518.5波動率期限結構與波動率曲面396...
附錄19a由波動率微笑確定隱含風險中性分布302第20章基本數值方法30420.1二叉樹30420.2採用二叉樹來對股指、貨幣與期貨期權定價31020.3對於支付股息股票的二叉樹模型...
災難過後,驚魂未定的交易員們將這種極端現象稱為“波動率微笑”,這是市場發出的令人毛骨悚然的冷笑。 第5章 兇殘的法瑪食人魚 法瑪說,大量投資者在不懈地尋找...
17.14股票市場波動率小結推薦閱讀練習題作業題附錄17A泰勒級數展開和對沖參數第18章波動率微笑18.1為什麼波動率微笑對看漲期權與看跌期權是一樣的18.2貨幣期權...
3.3基於MATLAB的波動率微笑與隱含波動率數值實驗3.4基於C++與Excel Addin的隱含波動率數值實驗第4章蒙特卡羅方法期權定價數值實驗4.1理論基礎4.2基於Excel的數值實驗—...
一、波動率微笑二、敏感性參數的中性組合第三章 期權的二叉樹定價法第一節 二叉樹風險證券定價法第二節 二叉樹歐式期權定價法一、單期歐式期權定價...
6.11.3 隱含波動率微笑 401第7章 量化投資十問十答 405精彩節摘推薦序一很榮幸收到王小川博士的邀請,為其新書《Python與量化投資:從基礎到實戰》作序。王小川...
2.3 波動率微笑和波動率期限結構2.4 股票類衍生產品定價數值解2.5 股票類衍生產品定價函式2.6 股票類衍生產品敏感性及定價函式第3章 期權組合策略...
11. 曾偉,陳平,“波動率微笑、相對偏差和交易策略——基於非線性生滅過程的股票價格一般擴散模型”,《經濟學(季刊)》, 第7卷,第4期,2008年7月,1415-1436頁...
1.5.7 模型校驗方法、隱含波動率和波動率微笑331.5.8 期權價格與風險中性密度341.6 評註與延伸閱讀35參考文獻35第2章 單期模型的套利理論372.1 定義與預備37...
第4章 毛骨悚然的“波動率微笑”第5章 兇殘的法瑪食人魚第6章 狼就在門口第7章 金錢也數位化了第8章 四個火槍手第9章 “上帝保佑,未來會更好...
三、波動率估計與“波動率微笑” 四、期權定價的敏感度分析 第三節 二叉樹模型和蒙特卡洛模擬在期權定價中的套用 一、二項式期權定價模型 二、二叉樹期權定價在可...
遠期和期貨價格的決定、互換、期權市場的機制、期權的交易策略、Black-Scholes-Merton模型、波動率微笑、數值方法、在險值、信用風險、信用衍生產品、奇異期權、凸性...
第17章 波動率微笑第18章 風險價值第19章 利率期權第20章 奇異期權和其他非標準產品第2l章 信用衍生證券第22章 天氣、能源和保險衍生證券第23章 衍生品災難和...
股票期權的性質、期權交易策略、布萊克-斯科爾斯模型、希臘值及其套用、波動率微笑、風險價值度、特種期權及其他非標準產品、信用衍生產品、氣候和能源以及保險衍生產品...
17?2課後習題詳解(203)第18章波動率微笑(219)18?1複習筆記(219)18?2課後習題詳解(222)第19章基本數值方法(232)19?1複習筆記(232)19?2課後習題詳解(242)...
第16章 波動率微笑第17章 基本數值方法第18章 風險值第19章 估計波動率與相關性第20章 信用風險第21章 信用衍生品第22章 奇異期權...
第18章 波動率微笑(219)18.1 複習筆記(219)18.2 課後習題詳解(222)第19章 基本數值方法(232)19.1 複習筆記(232)19.2 課後習題詳解(242)...
第18章 波動率微笑(219) 18.1 複習筆記(219) 18.2 課後習題詳解(222) 第19章 基本數值方法(232) 19.1 複習筆記(232) 19.2 課後習題詳解(242) 第20章...
六、波動率與“波動率微笑”/68 七、Delta 中性策略/68 第五章 個股期權套利策略/70 一、合成策略/70 二、垂直價差策略/81 三、日曆價差策略/92 四、跨式...
ITO33是一家軟體公司,專門從事衍生工具尤其是可轉換債券和波動率微笑曲線(volatility smiles)的數學模型和數值解軟體的開發。 成員Tim Mills Tim Mills現任英國國家...
本書內容期權基本概念,到期權希臘字母及隱含和歷史波動率的理論和實際操作意義。...第27課深層次的理解波動率——歷史波動率和隱含波動率,波動率微笑曲線 ···...
波動率微笑之謎超越布萊克-斯科爾斯:開發期權局部波動率模型的競賽正確的模型是很難開發的第15章 去年之雪 / 302華爾街上的合併衣著變得隨意...
