基本介紹
- 中文名:法坐標系
- 外文名:normal coordinate system
- 適用領域:數理科學
- 所屬學科:數學
定義











指數映射





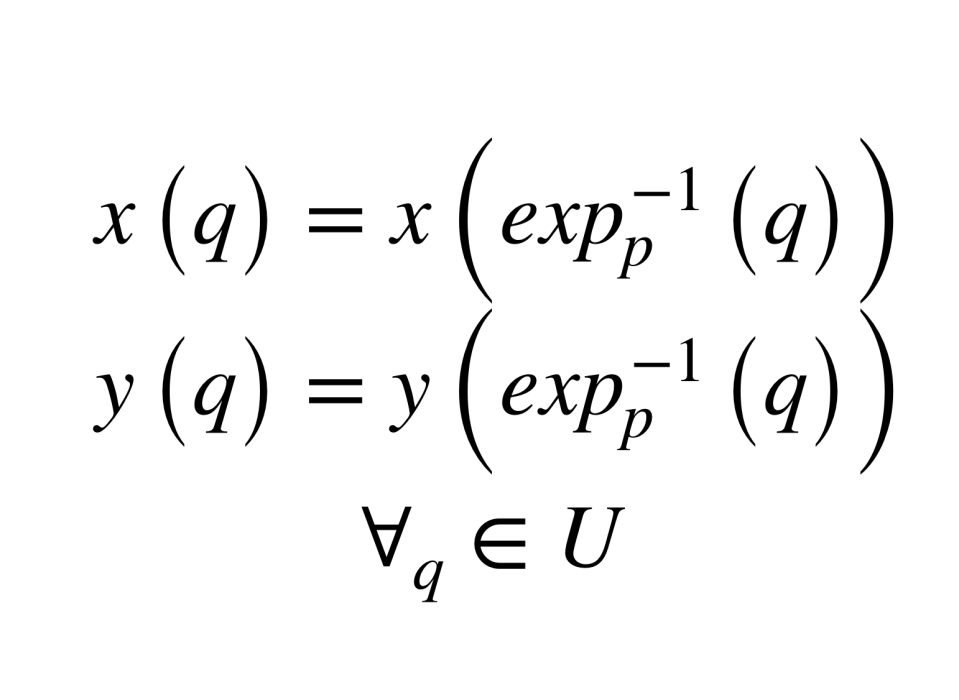
















法坐標系是曲面S上的一種特殊坐標系。指數映射和法坐標系是屬於曲面內蘊幾何學的概念,適用於任意維數的黎曼流形。定義對於每一點 ,都有一個正數 ,使得指數映射 是從切空間 在原點的鄰域 到曲面 S 在點 p 的鄰域 的可微同...
坐標系,是理科常用輔助方法,常見有直線坐標系,平面直角坐標系。為了說明質點的位置、運動的快慢、方向等,必須選取其坐標系。在參照系中,為確定空間一點的位置,按規定方法選取的有次序的一組數據,這就叫做“坐標”。在某一問題中...
坐標 ,數學名詞。是指為確定天球上某一點的位置,在天球上建立的球面坐標系。有兩個基本要素:①基本平面;由天球上某一選定的大圓所確定;大圓稱為基圈,基圈的兩個幾何極之一,作為球面坐標系的極。②主點,又稱原點;由天球上某...
平面坐標系的建立方法,數學用語。平面坐標系的建立方法 直角坐標網是以每一投影帶的中央經線為縱軸(X軸),赤道作為橫軸(Y軸),縱坐標以赤道為0起算,赤道以北為正,以南為負。橫坐標本來應以中央經線為0起算,以東為正,以西為...
極坐標法是在控制點上測設一個角度和一段距離來確定點的平面位置。方法介紹 不等同於笛卡爾直角坐標系中採用兩個正交軸的垂直投影進行定位(x,y),極坐標沒有X、Y軸,,坐標中某點表示為 D 幾何意義 用極坐標解決幾何問題的方法。
也可稱為真實世界的坐標系,是用於確定地物在地球上位置的坐標系。一個特定的地理坐標系是由一個特定的橢球體和一種特定的地圖投影構成,其中橢球體是一種對地球形狀的數學描述,而地圖投影是將球面坐標轉換成平面坐標的數學方法。絕大...
在許多工程測量中,其測量結果往往需要提供地方坐標系的坐標,這時就需要我們把GPS測量的處理結果從WGS84坐標系轉換到地方坐標系中。坐標轉換從方法上講有格網法、多參數法、多元回歸法等。參數法轉換模型一般有布爾莎模型、莫洛金斯基...
坐標系所在平面叫做坐標平面,兩坐標軸的公共原點叫做直角坐標系的原點。X軸和Y軸把坐標平面分成四個象限,右上面的叫做第一象限,其他三個部分按逆時針方向依次叫做第二象限、第三象限和第四象限。象限以數軸為界,橫軸、縱軸上的點不...
通常所套用的坐標系,如笛卡爾坐標系,是以【數值】數據建立的坐標系。二進制空間坐標系,是基於二進制【位值】數據建立的坐標系。定義 1、【坐標軸】的定義:(X,Y,Z)坐標的數軸“刻度”,稱為一個二進制序列【位】,每一個【...
設V是實n維線性空間,A是關於V的仿射空間,A中一個固定點O與V的一個基(e1,e2,e3)稱為A的一個仿射坐標系,O稱為坐標系的原點,於是對於A中每一點必有(x,y,z)稱為P點關於給定坐標系的仿射坐標。坐標系 坐標法的基礎是建立...
笛卡爾坐標系(Cartesian coordinates,法語:les coordonnées cartésiennes)就是直角坐標系和斜坐標系的統稱。相交於原點的兩條數軸,構成了平面仿射坐標系。如兩條數軸上的度量單位相等,則稱此仿射坐標係為笛卡爾坐標系。兩條數軸互相...
坐標軸(coordinate axis)用來定義一個坐標系的一組直線或一組線;位於坐標軸上的點的位置由一個坐標值所唯一確定,而其他的坐標軸上的點的位置由一個坐標值所唯一確定,而其他的坐標在此軸上的值是零。定義 1.用來定義一個坐標系的...
國家大地坐標系是測制國家基本比例尺地圖的基礎。根據《中華人民共和國測繪法》規定,中國建立全國統一的大地坐標系統。建國以來,中國於上世紀50年代和80年代分別建立了1954年北京坐標系和1980西安坐標系,測制了各種比例尺地形圖,在國民...
為了直觀的表達六方晶系中的晶向指數和晶面指數,因此建立四軸坐標系。指數限定法 由於在平面中,兩個坐標確定平面上的一點,所以四軸坐標系底面的三個坐標軸里只有兩個坐標軸是獨立的,因此我們將底面的三個坐標軸數值做出限定,防止一...
相對坐標系是在一個國家或一個地區範圍內統一規定地圖投影的經緯線作為坐標軸,以確定國家或某一地區所有測量成果在平面或空間上的位置的坐標系統。平面直角坐標 平面直角坐標系的概念 在平面“二維”內畫兩條互相垂直,並且有公共原點的...
笛卡兒坐標系(Cartesian coordinates,法語:les coordonnées cartésiennes)就是直角坐標系和斜坐標系的統稱。定義 標系稱為笛卡兒直角坐標系。人們經常把笛卡兒直角坐標系簡稱為笛卡兒坐標系。空間一點在笛卡兒直角坐標系中的位置分量稱為...
平面仿射坐標(affine coordinates in plane)是一種平面坐標,平面上取兩條相交的軸x與y,交點O稱為原點,在兩軸上各取一個單位點E₁,E₂,使x軸和y軸都成為坐標軸,對於平面上的任意點M,過M作兩軸的平行線,設它們與軸x,...
高斯平面坐標系,指的是以中央子午線與赤道的交點作為坐標原點,以中央子午線的投影為縱坐標軸X,規定X軸向北為正,以赤道的投影為橫坐標軸Y,Y軸向東為正,形成的坐標系。簡介 高斯平面直角坐標系是以赤道和中央子午線的交點作為坐標...
σ坐標 σ坐標是2009年公布的大氣科學名詞。定義 以σ=p/ps或類似的形式為垂直坐標的坐標系(p為氣壓,ps為地面氣壓)。出處 《大氣科學名詞》。
在數控編程時為了描述工具機的運動,簡化程式編制的方法及保證記錄數據的互換性,數控工具機的坐標系和運動方向均已標準化,ISO和我國都擬定了命名的標準。 工具機坐標系( Machine Coordinate System )是以工具機原點O為坐標系原點並遵循右手笛卡爾...
′是測點在局部坐標系中的位置矢量;m是尺度改正數;R是一個旋轉矩陣,它的元素是獨立的歐拉角εx、εy、εz,表示圍繞局部坐標系x、y、z軸的旋轉。計算這些轉換參數至少要有3個公共點,它們在兩種坐標系中的位置都是已知的。由此法...
工件坐標系是編程時使用的坐標系,又稱編程坐標系,該坐標系是人為設定的。建立工件坐標系是數控車床加工前的必不可少的一步。不同的系統,其方法各不相同。建立方法 通過試切對刀法 建立工件坐標系(以在右端面建立工件坐標係為例)...
由1954北京坐標系的大地坐標轉換到WGS-84的大地坐標,就屬於不同橢球體間的轉換。不同橢球體間的坐標轉換在局部地區的採用的常用辦法是相似變換法,即利用部分分布相對合理高等級公共點求出相應的轉換參數。一般而言,比較嚴密的是用七...
他對現代數學的發展作出了重要的貢獻,由於他的幾何坐標系的公式化而被認為是解析幾何之父。他還是西方現代哲學思想的奠基人之一,是近代唯心論的開拓者,提出了“普遍懷疑”的主張。他的哲學思想深深影響了之後的幾代歐洲人,並為歐洲的...
右手系(right-hand system)是在空間中規定直角坐標系的方法之一。此坐標系中x軸,y軸和z軸的正方向是如下規定的:把右手放在原點的位置,使大拇指,食指和中指互成直角,把大拇指指向x軸的正方向,食指指向y軸的正方向時,中指所指...
經緯度是經度與緯度組成的坐標系統,是一種利用三度空間的球面來定義地球上的空間的球面坐標系統,能夠標示地球上的任何一個位置。緯線 緯線和經線一樣是人類為度量方便而假設出來的輔助線,定義為地球表面某點隨地球自轉所形成的軌跡。任...
