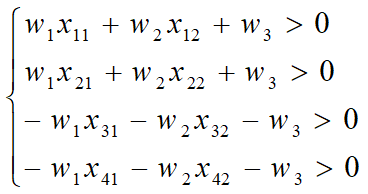決策函式

假設對一模式，已抽取d個特徵，表示為x=(x₁,x₂,....,x_d)^T。

x是d維空間的一個向量。

模式識別問題就是根據模式的d個特徵來判別模式屬於w₁,w₂..,w_c類中的哪一類。

例如下圖：三類的分類問題，它們的邊界線就是一個決策函式。

基本介紹

• 中文名：決策函式
• 外文名：decision function
• 學科：數學
• 本質：模式識別問題、分類問題
• 別稱：判決函式
• 相關名詞：模式識別

簡介

假設對一模式已抽取d個特徵，表示為

x是d維空間的一個向量。

模式識別問題就是根據模式的d個特徵來判別模式屬於 類中的哪一類。

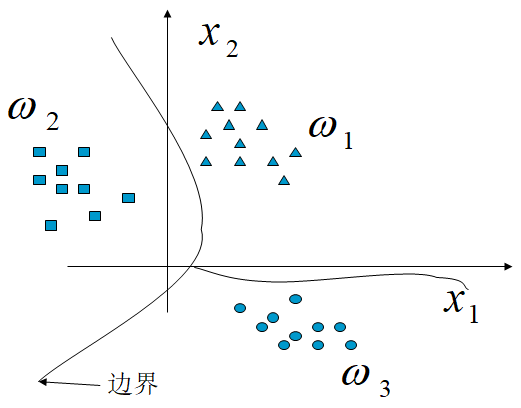
例如下圖：三類的分類問題，它們的邊界線就是一個決策函式。

分類

判決函式包含兩類： 一類是線性判決函式，具體包括：

（1）線性判決函式

（2）廣義線性判決函式（所謂廣義線性判決函式就是把非線性判別函式映射到另外一個空間變成線性判決函式）

（3）分段線性判決函式

另一類是非線性判決函式。

我們現在對兩類問題和多類問題分別進行討論。

(一)兩類問題 即:：

1. 二維情況 ：取兩個特徵
   

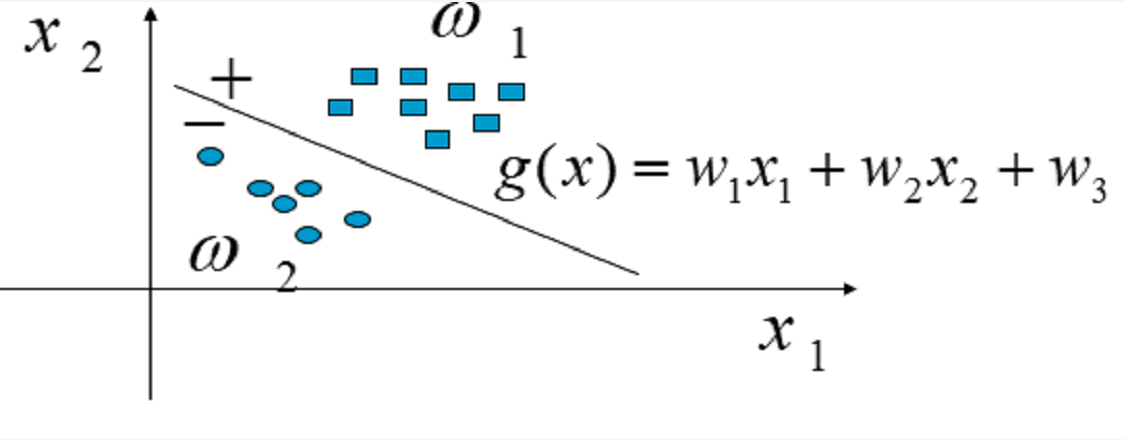
這種情況下，判決函式：

w為參數，x1,x2為坐標值。

在兩類別情況，判決函式 g (x) 具有以下性質：

這時二維情況下判決由判決邊界分類，情況如圖：

現抽取d個特徵為：

判決函式：

W₀為權向量，x為模式向量。

模式分類：

當 g₁(x) =W^TX=0 為判別邊界 。當d=2時，二維情況的判別邊界為一直線。當d=3時，判別邊界為一平面，d>3時，則判別邊界為一超平面。

(二)多類問題

對於多類問題，模式有 個類別。可分三種情況：

第一種情況：每一模式類與其它模式類間可用單個判決平面分開。這種情況，c類可有c個判別函式，且具有以下性質：

式中，W_i為第i個判別函式的權向量。

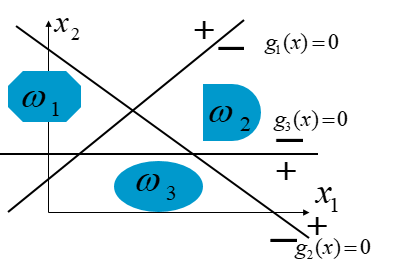
1. 第一種情況
   如下圖所示，每一類別可用單個判別邊界與其它類別相分開 。 如果一模式X屬於ω1，則由圖可清楚看出:這時g1(x) >0而g2(x) <0 ， g3(x) <0 。 ω1 類與其它類之間的邊界由g1(x)=0確定。
   

2. 第二種情況：

每個模式類和其它模式類間可分別用判決平面分開。這樣 有 c(c -1)/2個判決平面。

對於兩類問題，c=2，則有一個判決平面。 同理，三類問題則有三個判決平面。

判決函式：

判決邊界：

判決條件：

3.第三種情況

對c個類型中的每個類型都建立一個判決函式：

為了區分其中的某個類型 ，需要k個判決函式(k<=c)。

如果滿足：

則判：

對於不同的類型，k的取值可能不同。

判決規則：

就是說，要判決模式x屬於那一類，先把x代入k個判決函式中，判決函式最大的那個類別就是x所屬類別。 類與 類之間的邊界可由 gi(x) =gj(x) 或gi(x) -gj(x) =0來確定。

線性判決函式的性質

1、模式空間與加權空間

模式空間：由 構成的d+1維歐氏空間。

W是此空間的加權向量，它決定模式的分界面H，W與H正交。

加權空間：以 為變數構成的歐氏空間，模式空間與加權空間的幾何表示如下圖：

2、解向量和解區

在三維空間裡，令w3 = 0，則為二維權空間。如下圖。

給定一個模式x，就決定一條直線：

即分界面H，W與H正交，W稱為解向量。

解向量的變動範圍稱為解區。

因x1,x2∈ω1， x3,x4∈ω2由圖可見x1,x3離的最近，所以分界面H可以是x1,x3之間的任一直線，由垂直於這些直線的W就構成解區，解區為一扇形平面，即陰影區域。

把不等式方程正規化：

正規化：

3、超平面的幾何性質

g(x)=WT x=0決定一個決策界面，當g(x)為線性時，這個決策界面便是一個超平面H，並有以下性質：

性質①：W與H正交

性質 ②：

性質③：

廣義線性判決函式：

判決函式的一般形式：

式中，是單值函式，