《氣動聲學》是1952年由萊特希爾在英國皇家學會會刊上發表的一篇研究流體發聲機理的論文。
基本介紹
- 中文名:氣動聲學
- 外文名:Aeroacoustics
- 創始人:萊特希爾
- 類別:聲學學科
- 缺點:聲源項未知,因此需要模化
產生簡介
方程推導
噪聲源
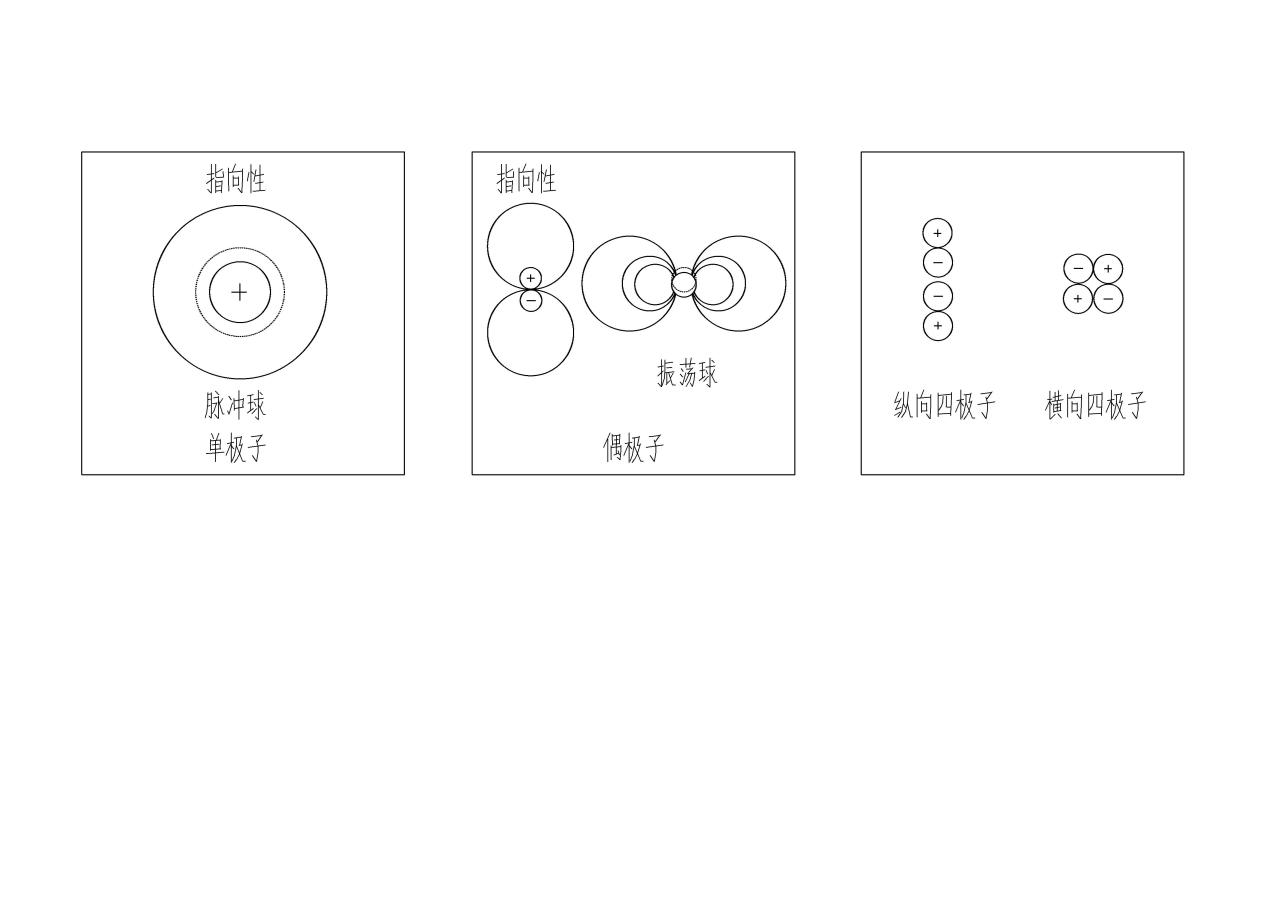
噪聲源


《氣動聲學》是1952年由萊特希爾在英國皇家學會會刊上發表的一篇研究流體發聲機理的論文。


《氣動聲學》是1952年由萊特希爾在英國皇家學會會刊上發表的一篇研究流體發聲機理的論文。...
1952年由萊特希爾在英國皇家學會會刊上發表了一篇研究流體發聲機理的論文,在這篇論文中,他推導了後來以他名字所命名的方程,人們普遍把這項工作當作氣動聲學誕生的...
《氣動聲學》由國防工業出版社於1994年出版,由孫曉峰等編著。 [1] 本書主要講述 內容包括運動介質中的聲場、氣動聲學的基本方程、螺旋漿聲學、渦聲理論等9章。
計算氣動聲學(CAA)是基於計算流體力學與氣動聲學的交叉學科,採用數值計算的方法研究流體與固體邊界間相互作用所產生的噪聲的非定常流動機理,以便對於噪聲的預測與改善...
《氣動聲學基礎》是2012年9月國防工業出版社出版的圖書,作者是張強。...
中文名稱 氣動聲學設計 英文名稱 aeroacoustic design 定義 在保證發動機總體性能前提下,以發動機可能的最低噪聲級為目標進行的聲學設計。 套用學科 航空科技(一級...
CAA (計算氣動聲學) 編輯 討論 上傳視頻 本詞條缺少信息欄、概述圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧! CAA是計算氣動聲學,基於計算流體力學與...
《航空發動機氣動聲學》從氣動力學和氣動聲學的基本理論出發,研究當代先進航空燃氣渦輪發動機氣動噪聲產生的物理機制,系統分析航空發動機氣動噪聲的基本特徵;通過對國內外...
航空氣動聲學工業和信息化部重點實驗室是2017年工業和信息化部重點實驗室,依託於北京航空航天大學。 ...
《車用渦輪增壓器的氣動與振動聲學》是2019年5月國防工業出版社出版的圖書,作者是[德]雄阮-舍費爾。...
風洞試驗是開展氣動噪聲產生機理研究的重要手段,也是驗證氣動降噪最佳化設計最直接、有效的方法。氣動聲學試驗最主要的目的是精確地測定出氣動噪聲源產生的區域,並測得聲...
第3章為格線最佳化的迎風型色散保持氣動聲學格式;改進的聲擾動方程及其數值驗證;第4章為基於格子Boltzmann方法的氣動聲學計算方法,完善並研究了格子Boltzmann方法,改進了...
《Virtual.Lab Acoustics聲學仿真計算》是2010年8月國防工業出版社出版的圖書,作者是李增剛、詹福良。...
內容涉及汽車、發動機、消聲器、飛機等,主要包括聲學有限元、聲學邊界元、聲學無限元、PML方法、多級邊界元、ATV和MATV、傳遞損失、氣動聲學、瞬態有限元和瞬態邊界...
本書可作為大學高年級學生和研究生課程的教科書,也可作為水聲學、結構聲學以及氣動聲學等領域中從事近場聲全息、近場/遠場聲輻射、聲成像、聲場可視化、傳聲器陣列...
4.5.1 計算氣動聲學4.5.2 計算氣動彈性4.5.3 飛機結冰計算第5章 空氣動力設計技術5.1 概述5.2 飛機設計5.2.1 飛機設計的內容和階段...
computational aeroacoustics 計算氣動聲學 ; 計算氣動聲學方法 nonlinear aeroacoustics 非線性航空聲學 International Journal of Aeroacoustics 國際空氣聲學雜誌...
inverse aeroacoustic problem 氣動聲學反問題 aerodynamic and aeroacoustic performance 氣動 aerodynamic-aeroacoustic performance 氣動──聲學性能 [1] aero...
賴煥新,2006.09-Present,華東理工大學,教授,博士生導師 [1] 。 研究方向包括計算流體動力學(CFD)、計算氣動聲學(CAA)、流體機械內流 化工流體力學。
主講氣動聲學與噪聲控制(本科)、基礎聲學(研究生)、計算氣動聲學(研究生)三門課程。 [1] 高軍輝研究方向 編輯 感興趣的研究領域包括噴流噪聲、機體噪聲和高精度...
2001年5月 - 2002年4月 高級訪問學者,德國宇航院(DLR)柏林湍流研究分部,從事航空發動機和飛機非定常流動、氣動聲學的研究。2007年8月 - 2007年9月 高級訪問...
北京大學工學院航空航天系低噪聲飛行器實驗室,隸屬於工學院,成立於2009年,主要研究氣動聲學、流動控制、飛行器控制,依託北京大學文理醫工綜合基礎,根據國家迫切需要的...
螺旋槳風洞螺旋槳風洞實驗氣動聲學相似準則 編輯 通常情況下,無論是螺旋槳的氣動力特性測量還是噪聲特性測量都是用縮尺模型在比較小型的低速風洞中進行。要使縮尺模型...
