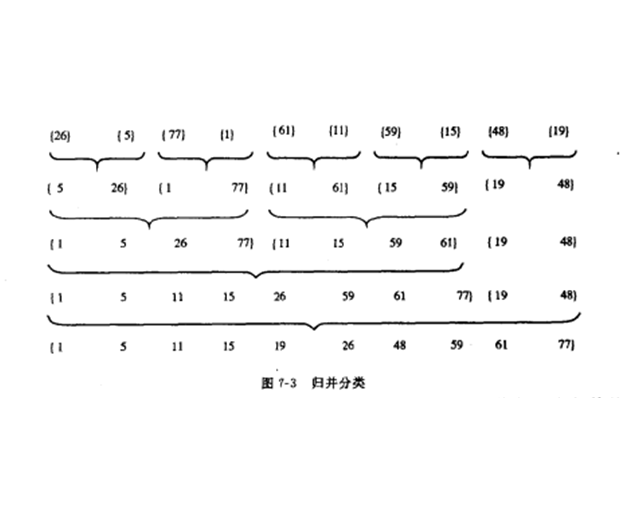
分類技術根據記錄所處的環境不同而分為內部分類和外部分類兩大類。內部分類是指分類期間全部數據都存放在記憶體的分類方法；外部分類則是針對大量記錄而言的，分類期間，全部記錄已不能同時存放在記憶體，需要記錄在內、外存之間移動。歸併分類是分治法中的一種算法，屬於內部分類技術。若果用分治策略來設計分類算法，則可使最壞情況下時間變為O(nlogn)，這樣的算法稱為歸併分類算法，也稱為二路歸併分類算法。
基本介紹
- 中文名：歸併分類
- 外文名：Merge sort
- 別名：二路歸併分類
- 算法策略：分治策略
- 時間複雜度：O(nlogn)
- 缺點：分類效率不高
定義,分類,檔案的物理表示法,分類技術,算法,基本思想,程式,算法分析,改進的歸併分類算法,改進算法1,改進算法2,
定義
分治法的思想是將一個難以直接解決的問題分解成容易求解的子問題，以便各個擊破、分而治之。利用分治法求解問題的過程是，將整個問題分解成若干子問題後分而治之；如果分解得到的子問題仍然不易求解，可反覆使用分治策略將這些子問題分成更小的子問題，直至產生出容易求解的子問題，最後逐步合成這些子問題的解，以得到問題的解。歸併分類就是分治法中的一種算法。
分類
分類問題就是按照關鍵值的一種排序關係，如大於關係。如根據關鍵值的不增或不減次序，把檔案中的各種記錄一次排列起來，可使得一個無序檔案變成有序檔案。
檔案的物理表示法
（1）向量表示。要分類的初始檔案的各個記錄，按其自然順序存放在連續一塊記憶體空間中。
（2）鍊表表示。要分類檔案的每個記錄作為鍊表結構的一個結點，並按照各個記錄的原始次序連結起來。
（3）地址向量。將要分類檔案的各個記錄存貯到記憶體的各塊中，這些存貯塊的地址是不連續的。按各記錄的原始次序，將這些塊的首地址依次存如記憶體的一塊連續單元中，這樣由各塊的首地址組成一個向量，這個向量就是地址向量。
分類技術
分類技術根據記錄所處的環境不同而分為內部分類和外部分類兩大類。內部分類是指分類期間全部數據都存放在記憶體的分類方法；外部分類則是針對大量記錄而言的，分類期間，全部記錄已不能同時存放在記憶體，需要記錄在內、外存之間移動。常見的幾種內部分類技術包括：
（1）計數分類。主要思想是對於每個記錄，都要計算檔案中其它記錄的關鍵字值有多少是大於該記錄的關鍵字值，從而找到這個記錄的正確分類位置，這是一種效率較低的分類方法。
（2）選擇分類。以教師對學生的考試成績按分數進行分類為例，首先找到成績最好的試卷，並把它出來，作為新一疊試卷的頭一份試卷，然後在剩餘的試卷中再選出分數最高的試卷，並把它放在新的那疊試卷之上，如此繼續下去，最後就完成了按分數高低分類這些試卷，這個過程即為選擇分類。
（3）冒泡分類。每一次僅進行相鄰兩個記錄的比較，使位於檔案底部的合適記錄一下子放到檔案的頂部，而只能每次向上移動一步，緩慢升到頂部，因此一個檔案的全部分類是由多次重複比較相鄰記錄的關鍵字而實現的。
（4）線性插入；將原始檔案順序的第二個記錄的關鍵字與第一個記錄的關鍵字進行比較後，把第二個記錄放到一個相對於第一個記錄的合適位置。然後再取第三個記錄於前二個記錄進行比較關鍵字，並把第三個記錄放到相對於前兩個記錄的合適位置，如此繼續下去，最後完成分類。
（5）折半插入，它是線性插入的改進。
（6）歸併分類，兩個分類檔案的歸併問題和k個分類檔案的歸併問題。
算法
基本思想
設待分類的數據序列包含n個數據元素。
（1）先把該序列分成n個子序列，每個子序列只包含一個數據，顯然，這n個子序列都是有序的；
（2）將這n個子序列兩個一組，可分成（n+1）/2（取整）個互不相交的組；
（3）對每個組的2個子序列進行二路歸併，總共得到（n+1）/2個有序子序列；
（4）對這些有序子序列兩個一組，對每個組進行二路歸併。
如此繼續下去，最後得到一個有序的結果序列。
程式
# include "sort.h"
getdata(int a[]);
void output(int a[],int first,int last);
void mersort(int a[],int b[],int s,int t);
void merge(int a[],int l,int m,int n,int c[]);
void main(){
int arr[MAX],arrb[MAX],n;
n=getdata(arr);
output(arr,l,n);
printf("\n");
mersort(arr,arrb,l,n);
output(arrb,l,n);
printf("\n");
}
void mersort(int a[],int b[],int s,int t){
int i;
if(s==t)return;
else{
mersort(a,b,s,(s+t)/2);
mersort(a,b,(s+t)/2+1,t);
mersort(a,s,(s+t)/2,t,b);
for(i=s;i<=t;i++)
a[i]=b[i];
}
}
}
void merge(int a[],int l,int m,int t,int c[]){
int i,j,k,i1;
i=l;
j=m+1;
k=l-1;
while(i<=m && j<=n){
k++;
if(a[i]<=a[j]){
c[k]=a[i];
i++;
}
else{
c[k]=a[j];
j++;
}
}
if(i<=m)
for(i1=k+1,i1<=n;i1++){
c[i1]=a[i];
i++;
}
if(j<=n)
for(i1=k+1;i1<=n;i1++){
c[i1]=a[j];
j++;
}
}
算法分析
歸併分類算法時間複雜度為O(nlogn)。歸併分類方法相當充分地反映了使用分治策略對數據對象分類的長處，但是仍存在一些明顯的不足，從而限制了分類效率的進一步提高。
首先，每當計畫被分為只含有兩個元素的子集合時，還需要使用二次遞歸調用將這子集合分成單個元素的集合。這表明該算法執行到將集合分成含元素相當少的子集合時，很多時候不是用在實際的分類，而是消耗在遞歸外了。
另外，歸併算法使用了輔助數組，這是一個明顯的不足之處，但是由於不可能在兩個已分類集合的原來位置上進行適當的歸併，所以這n個位置的附加空間對於本算法是必須的，不過，使用一個以整數表示的鍊表信息數組來代替輔助數組可以節省一些附加空間。
改進的歸併分類算法
改進算法1
使用連結的歸併分類模型，，其主要算法如下：
MERGESORT1 (A,low,high,p)
if high-low+1<16
then INSERTIONSORT (A,LINK,low,high,p)
else{
mid=(low+high)/2; /*求這個集合的分割點*/
MERGESORT1 (low,mid,p); /*返回q表*/
MERGESORT1 (mid+1,high,r); /*返回r表*/
MERGE1 (q,r,p) /*將表q和r歸併成表p*/
在這個算法中，利用輔助數組LINK[low:high]將全長數組A[low:high]按非降次序分類。LINK中值表示按分類次序給出A下標的表，並將p置於指示這表開始處。
改進算法2
使用連結表歸併已分類的集合，其主要算法如下：
MERGE1 (A,p,r,q)
i=q;
j=r;
k=0;
while i≠0 and j≠0
do{
if A[i]<=A[j]
then{
LINK[k]=i;
k=i;
i=LINK[i];
}
else{
LINK[k]=j;
k=j;
j=LINK[j];
}
}
if i=0
then LINK[k]=j;
else
LINK[k]=i;
p=LINK[0];
