基本介紹
- 中文名:基礎算法
- 外文名:fundamental algorithm
- 套用學科:計算機科學
- 包含:快速排序算法、堆排序算法等
- 適合領域範圍:C/C++/java等
- 性能指標:平均時間複雜度
快速排序算法
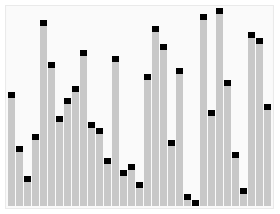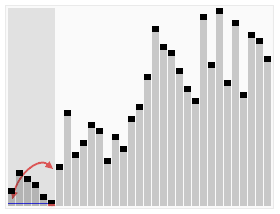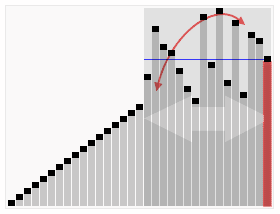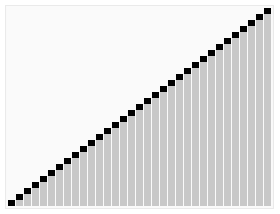 快速排序算法
快速排序算法堆排序算法
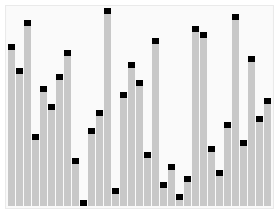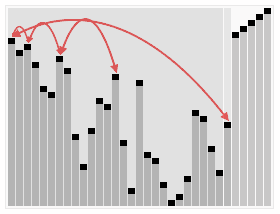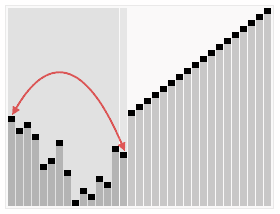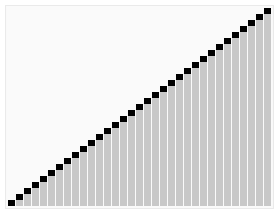 堆排序算法
堆排序算法歸併排序
 歸併排序
歸併排序二分查找算法
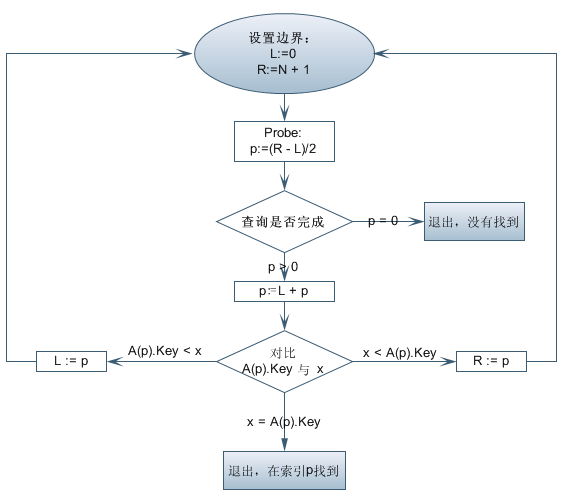 二分查找算法
二分查找算法BFPRT(線性查找算法)
DFS(深度優先搜尋)
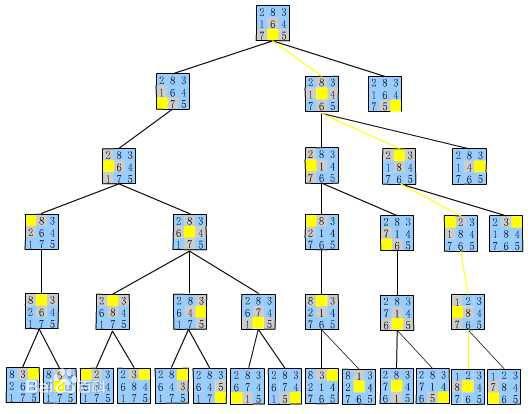 DFS(深度優先搜尋)
DFS(深度優先搜尋)BFS(廣度優先搜尋)
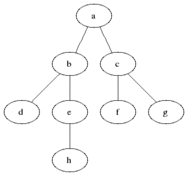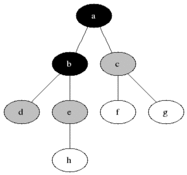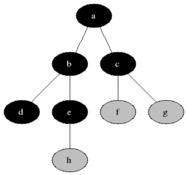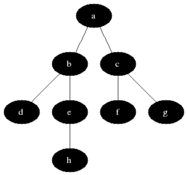 BFS(廣度優先搜尋)
BFS(廣度優先搜尋)Dijkstra算法


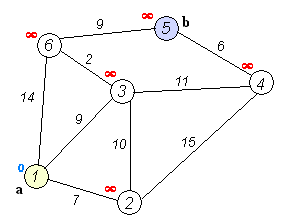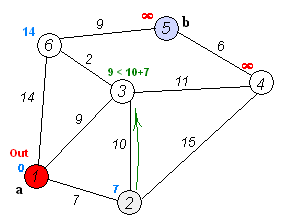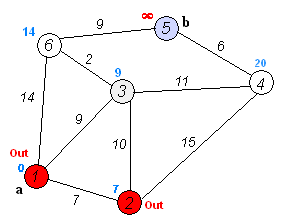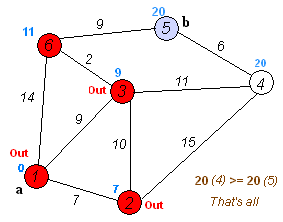 Dijkstra算法
Dijkstra算法
 快速排序算法
快速排序算法 堆排序算法
堆排序算法 歸併排序
歸併排序 二分查找算法
二分查找算法 DFS(深度優先搜尋)
DFS(深度優先搜尋) BFS(廣度優先搜尋)
BFS(廣度優先搜尋)

 Dijkstra算法
Dijkstra算法算法是一個程式和軟體的靈魂,要成為一名優秀的程式設計師,只有對基礎算法全面掌握,才能在設計程式和編寫代碼的過程中顯得得心應手。常用的基礎算法有快速排序算法、堆...
算法(Algorithm)是指解題方案的準確而完整的描述,是一系列解決問題的清晰指令,算法代表著用系統的方法描述解決問題的策略機制。也就是說,能夠對一定規範的輸入,在...
《算法基礎》是2005年7月1日清華大學出版社出版的圖書,作者是布拉薩德。本書適用對象廣泛。對於學習算法設計與分析的本科生和研究生。...
《計算機圖形學的基礎算法》是2007年科學出版社出版的圖書,作者是劉勇奎。... 《計算機圖形學的基礎算法》是2007年科學出版社出版的圖書,作者是劉勇奎。...
《數據結構與算法基礎》是2000年大連理工大學出版社出版的圖書,作者是李蓮治。... 《數據結構與算法基礎》是2000年大連理工大學出版社出版的圖書,作者是李蓮治。...
算法可以理解為由基本運算及規定的運算順序所構成的完整的解題步驟,或者看成按照要求設計好的有限的確切的計算序列,並且這樣的步驟和序列可以解決一類問題。一般算法有...
《科學計算方法基礎》是2006年清華大學出版社出版的圖書,作者是李慶揚。本書強調方法的構造與套用,既重視理論分析,又避免過多的理論證明。...
基本運算是指執行運算最基礎的算法。在關係代數運算中,有5種基本運算,它們是並(U)、差(—)、投影、選擇、笛卡爾積(X),其它運算即交、連線和除,均可通過5種...
《算法基礎:打開算法之門》是2015年12月由機械工業出版社出版的一本圖書。... 《算法基礎:打開算法之門》是2015年12月由機械工業出版社出版的一本圖書。 [1] ...
《程式設計與算法基礎》是1999年黃河水利出版社出版的圖書,作者是張堯。... 《程式設計與算法基礎》是1999年黃河水利出版社出版的圖書,作者是張堯。...
《算法設計方法》一書介紹了算法描述和算法分析的基本方法,詳細介紹了各種典型算法的基本設計思路。算法是計算機科學的核心內容之一,也是套用電子計算機求解實際問題的...
,從幾何與計算兩個基本要素分析圖學計算的若干關鍵問題,給出圖學的計算基礎。...附錄A 圖學計算基礎算法索引161附錄B 判斷計算參數的一些約定181...
本書示例豐富,圖文並茂,以讓人容易理解的方式闡釋了算法,旨在幫助程式設計師在日常項目中更好地發揮算法的能量。書中的前三章將幫助你打下基礎,帶你學習二分查找、...
(3)網路模型與算法研究。在理論模型研究的基礎上構作具體的神經網路模型,以實現計算機模擬或準備製作硬體,包括網路學習算法的研究。這方面的工作也稱為技術模型研究...
《算法語言與計算方法基礎》是2005年北京科學出版社出版的一本書。該書是一本集算法、程式設計和數學模型實例於一體的新型教材。...
“智慧型算法”是指在工程實踐中,經常會接觸到一些比較“新穎”的算法或理論,比如模擬退火,遺傳算法,禁忌搜尋,神經網路,天牛須搜尋算法等。這些算法或理論都有一些...
《算法之道》是2010年2月機械工業出版社出版發行的圖書,作者是鄒恆明。... 《算法之道》將算法的討論分為五大部分:算法基礎篇、算法設計篇、算法分析篇、經典算法...
在數學和計算機科學之中,算法(Algorithm)為一個計算的具體步驟,常用於計算、數據處理和自動推理。精確而言,算法是一個表示為有限長列表的有效方法。算法應包含清晰...
計算機語言只是一種工具。光學習語言的規則還不夠,最重要的是學會針對各種類型的問題,擬定出有效的解決方法和步驟即算法。有了正確而有效的算法,可以利用任何一種...
所謂算法是指在有限步驟內求解某類問題所使用的一組定義明確的規則。算法重在用一個統一的方法有步驟地解決一類問題,但它不是唯一的,一個好的算法應該用較少的...
ERP算法的基本邏輯可以分以下幾個方面,如下圖所示: [1] 1、確定需要什麼產品,生產量是多少。2、通過BOM分解生產這些產品需要哪些物料。...
算法學,英文名稱algorithmics,系統地研究算法的設計、分析和驗證的學科。現在計算機問世以來,人們不斷用計算機求解一些空前大型和複雜的數學問題,與計算機打交道,即是...
多項式算法(polynomial algorithm)亦稱有效算法或好算法,是一類計算時間不超過始數據量的一個多項式的算法,算法滿足以下的條件:存在多項式P,使算法的時間複雜性函式f(...
《零基礎學大數據算法》通俗易懂的大數據算法教程。通篇採用師生對話的形式,旨在用通俗的語言、輕鬆的氣氛,幫助讀者理解大數據計算領域中的基礎算法和思想。...
對算法的學習包括5個方面:設計算法、表示算法、確認算法、分析算法、驗證算法。算法設計工作是不可能完全自動化的,應學習了解已經被實踐證明有用的一些基本的算法設計...
《數據結構基礎》是2008年7月機械工業出版社出版的圖書,作者是史九林。本書主要介紹了數據結構基礎知識和常見算法設計技術。...
《圖解算法》是2017年9月機械工業出版社出版的圖書,作者是俞征武。... 本書以輕鬆的對話方式,採用圖解的輔助說明,幫助讀者簡單、自然地掌握算法的基本概念,並養成...
啟發式算法(heuristic algorithm)是相對於最最佳化算法提出的。一個問題的最優算法求得該問題每個實例的最優解。啟發式算法可以這樣定義:一個基於直觀或經驗構造的算法...
