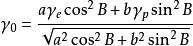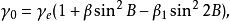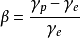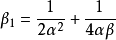正常橢球(水準橢球)面上的重力稱為正常重力。正常重力值可由正常重力公式計算求得，正常重力值只與緯度有關，與經度無關，其極大值在兩極，極小值在赤道。
假設地球是一個密度均勻而且光滑的理想橢球體，或是一個密度成層分布的光滑橢球體，在同一層內密度是均勻的、各層的界面也都是共焦旋轉橢球面，則球面上各點的重力位或重力值可以根據地球的引力參數、地球長半徑、扁度、自轉角速度等計算得出，由此計算出的重力值稱為正常重力值。
基本介紹
- 中文名：正常重力
- 外文名：normal gravity
- 條件：正常橢球面
- 注釋：正常重力場中的重力
- 套用：地球物理測量
- 性質：理論模型
簡要介紹,公式計算,問題與對策,
簡要介紹
正常橢球(水準橢球)面上的重力稱為正常重力。正常重力值可由正常重力公式計算求得，正常重力值只與緯度有關，與經度無關，其極大值在兩極，極小值在赤道。
重力在地表上變化的原因主要有：
- 地球的實際形狀比較複雜，是一個北極稍突出、南極稍縮入，赤道半徑較兩級半徑稍大的類似梨狀的扁球體，並且地面是起伏不平的；
- 地球繞一定的旋轉軸自轉；
- 地球內部、特別是地殼岩石圈層及其附近的物質密度分布不均勻，這是地球歷史上多次複雜的地質作用造成的結果。因此這個分布不均勻與地質構造、礦產分布有著密切的關係；
- 人類的歷史活動在接近地表形成的遺蹟和人工建築物體的存在，造成局部地區密度分布的微小不均勻變化。
從以上引起重力在地表變化的諸多原因可以知道，要根據地表重力變化來推測地下的密度分布以達到探查礦藏、研究地質構造的目的，就必須知道單純由地下介質密度分布不均勻所引起的重力變化。顯然，這樣就必須知道地下介質密度均勻情形下重力在地面上的分布規律。
假設地球是一個密度均勻而且光滑的理想橢球體，或是一個密度成層分布的光滑橢球體，在同一層內密度是均勻的、各層的界面也都是共焦旋轉橢球面，則球面上各點的重力位或重力值可以根據地球的引力參數、地球長半徑、扁度、自轉角速度等計算得出，由此計算出的重力值稱為正常重力值。這種情況下的重力場稱為正常重力場，表示正常重力場的數學解析式稱為正常重力公式。
公式計算
描述地球重力場規則部分的一種模型重力。即平均地球橢球，或稱正常橢球的重力，是正常重力位的梯度。若用γe表示赤道上的重力，γp表示極點的重力，a，b分別表示平均地球橢球的長、短半軸，則平均地球橢球面上地理緯度B處的正常重力為
這一公式是索米利亞納(Somigliana，C.)於1929年導出的，稱為索米利亞納正常重力公式。在套用中，一般將上式展開成級數：
式中
稱為重力扁率，
α為平均橢球體的扁率。在地球的正常重力場模型中，一般給出γe，β和β1三個值。
問題與對策
物理大地測量中作為正常場源的正常橢球卻只定義了長半軸、扁率、赤道重力、角速度及總質量等幾何量和表面物理量，其內部密度沒有確切的分布，這是物理大地測量本身的理論體系所決定的。因此，要使得物理大地測量與地球物理的相互交叉，聯合探求地球內部結構並解決密度反演中套用重力異常時所隱含的不確定性，首先就必須研究正常重力場源的同源性問題。
正常重力場的同源性問題歸結起來應該是，物理大地測量與地球物理分別（結果應具有可比性）或聯合用於反演內部密度結構的重力異常，其所對應的正常重力應產生於同一具有確切物理意義的正常場源（或理論模型）；而由外部重力場通過不同方法得到的內部密度異常所對應的正常密度應是同一的。
理論上，研究重力場的同源性問題有兩種途徑可循：大地重力學擾動邊值（如重力異常、重力擾動，擾動位等）不變，構制相應的正常場源。這須克服許多數學和物理上的困難。直接選用或改進已有的地球物理模型代替參考橢球，而將傳統的大地重力學擾動邊值加以改造。這將涉及到整個傳統的反演體系的調整。
將物理大地測量的正常場源與地球物理地球模型統一起來，是物理大地測量研究向地球內部拓展所面臨的主要問題之一，也是物理大地測量與地球物理學科交叉並對地球內部密度進行綜合解釋的真正基礎。由於這一問題涉及到學科界線及其傳統理論框架的突破，以及數學求解與物理解釋上的諸多困難，真正融合兩學科的物理實際所建立的有效模型尚未發現。本文所作研究即是對這一問題的初步探索，與許多為正常橢球賦值問題的不同之處，在於套用了地球物理中PREM模型的密度分布，使得聯合反演尤其是物理大地測量反演得到的地球內部密度解釋有了較為明確的物理意義。事實上，類似的做法，人們還可能選擇其他的約束（如來自於地震的波速場、自由振盪頻率等），來建立更有效的地球內部場源的統一模型。
