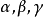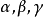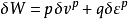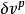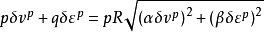正常壓密粘土

粘土壓密類型的概述

簡介

粘土的壓密類型及結構特性與其力學性質密切相關。最明顯的事實是反映在應力水平對力學性質的影響。例如在地基沉降計算中, 採用的變形參數的數值，對於不同壓密類型的土, 必須根據應力水平區別對待。在穩定性分析中, 採用的強度指標也依賴於固結應力水平和排水條件。處於欠壓密 , 正常壓密和微超壓密狀態的土，在三軸剪下時體積縮小排水或孔隙水壓力增大不排水，而處於超壓密狀態的土，剪下時體積膨脹排水或孔隙水壓力減小不排水，同時，土體結構強度的破損程度與固結應力水平有關。從本構關係來說，壓密狀態的不同和結構強度的存在，使本構關係由於應力水平不同而變化。

用壓密曲線的性態加以鑑別

若以正常固結線為基堆線 , 則可把形形色色的天然土樣的壓密曲線分為兩大類。一類為結構強度的影響可以忽略不計的粘土，一類為存在結構強度影響的粘土圖。每一類又可分為三種壓密類型，其命名和基本屬性簡單概括於下表中。

壓密類型	臨界壓力	先期固結壓力	超固結比R=pc/p0	天然圧密度
欠壓密土	pc	pc=pk	<1.0	<1.0
正常壓密土	pc	pc=pk	=1.0	=1.0
超壓密土	pc	pc=pk	>1.0	>1.0
有結構強度的欠壓密土	pk	pc<pk	<1.0	<1.0
有結構強度的正常壓密土	pk	pc<pk	=1.0	=1.0
有結構強度的超壓密土	pk	pc<pk	>1.0	>1.0

正常壓密粘土的方程

屈服面方程

早在羅斯格等於1963年提出屈服面成彈頭形的“劍橋粘土”模式後不久，我國科學家於1964年就根據不排水三軸壓縮試驗的應力路線資料得出，正常壓密粘土的屈服面在平均壓應力p和主應力差q的座標中一般成橢圓形。後來 , 羅斯格和柏蘭，考司拉和吳等也紛紛提出橢圓形的屈服面。實際上，前者是我們提出的一般形式的特殊情況 , 而後者則與我們提出的完全等同。

按照中性荷重（應力路線沿屈服面上移動）時塑性應變為零的定義出發，根據不排水應力路線的試驗資料得出屈服面的一般表達式為