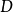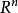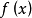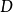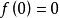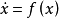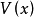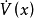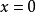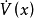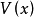正定函式是一個在許多領域都會遇到並且很有用的概念。如機率論中隨機變數的特徵函式就是正定函式。特徵函式比隨機變數的分布函式更易於處理。在Lyapunov穩定性理論中,Lyapunov函式的正定及其導數的負定說明了系統的穩定性。
基本介紹
- 中文名:正定函式
- 外文名:positive definite function
- 套用領域:數學
定義,套用,Lyapunov穩定性,
定義
設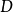 ⊂
⊂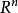 是包含原點的一個區域,如果定義在
是包含原點的一個區域,如果定義在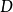 上的連續函式
上的連續函式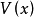 滿足:
滿足: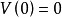 ,以及
,以及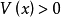 ,
,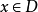 且
且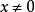 。則稱
。則稱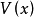 是正定的。如果只滿足弱一點的條件,對
是正定的。如果只滿足弱一點的條件,對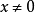 ,只有
,只有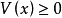 ,則稱
,則稱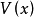 為半正定的。
為半正定的。
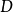
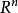
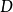
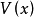
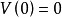
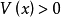
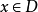
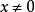
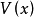
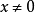
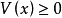
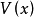
此外,如果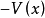 是正定的或者半正定的,則稱
是正定的或者半正定的,則稱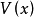 是負定的或者半負定的。如果不能斷定
是負定的或者半負定的。如果不能斷定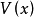 為四種情況中的某一種,則稱它是不定的。
為四種情況中的某一種,則稱它是不定的。
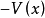
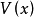
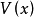
套用
Lyapunov穩定性
設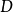 ⊂
⊂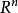 是包含原點的一個區域,
是包含原點的一個區域,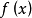 為定義在
為定義在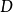 上滿足局部Lipschitz條件,且
上滿足局部Lipschitz條件,且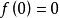 。對於系統
。對於系統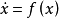 ,如果存在一個連續可微的正定函式
,如果存在一個連續可微的正定函式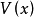 使得
使得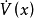 為半負定,則原點
為半負定,則原點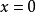 為系統的穩定平衡點。如果進一步使得
為系統的穩定平衡點。如果進一步使得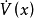 為負定的,則原點具有漸近穩定性;如果
為負定的,則原點具有漸近穩定性;如果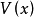 還滿足徑向無界,則原點具有全局漸近穩定性。
還滿足徑向無界,則原點具有全局漸近穩定性。