正則條件機率(The regular conditional probability)亦稱條件機率測度。
基本介紹
- 中文名:正則條件機率
- 外文名:The regular conditional probability
- 領域:統計學
- 別名:條件機率測度
- 性質:條件機率性
- 用途:條件機率的積分為條件期望
定義
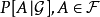
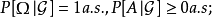
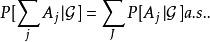
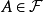
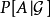
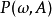
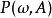
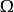
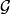
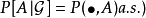
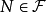
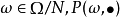
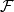

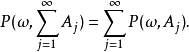
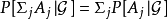
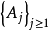
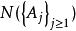


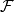
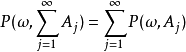
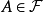
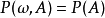
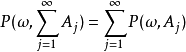
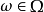


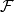
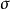
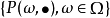
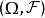
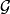
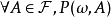
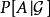
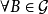
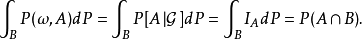
相關定理




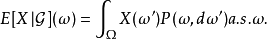
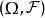
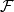
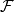
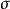

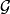
正則條件機率(The regular conditional probability)亦稱條件機率測度。
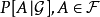
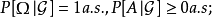
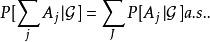
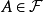
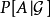
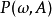
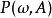
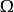
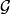
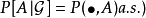
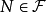
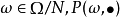
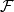

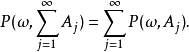
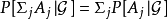
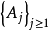
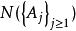


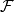
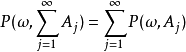
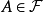
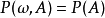
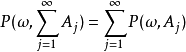
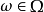


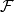
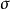
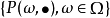
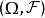
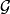
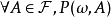
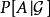
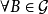
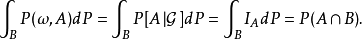




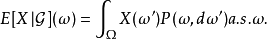
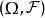
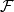
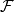
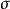

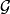
正則條件機率(The regular conditional probability)亦稱條件機率測度。...... 正則條件機率(The regular conditional probability)亦稱條件機率測度。中文名 正則條件機率 ...
正則條件是指在陳述某一個定理時,常常需要限定這些定理的使用範圍。如果超出這個範圍,則會導致定理所描述的內容不成立。用於限定這個使用範圍的限定條件被稱為“正則...
正則條件分布(regular conditional distribut -ion)是一類條件分布,指在0域留下的條件分布。...
《高等機率論基礎及極限理論》是2014年清華大學出版社出版的圖書,作者是胡澤春。...5.2.5正則條件機率 935.3隨機變數的一致可積性 .96第6章鞅論簡介 101...
《機率論基礎》是對本科階段所學機率論的嚴格化、抽象和延伸,幾個難點包括單調類定理、測度擴張定理、條件期望與正則條件機率,如何在學習中清楚地理解引入它們的背景...
Hausdorff空間上的測度與積分、測度的弱收斂和淡收斂,以及與測度論有關的機率論...7.3 正則條件機率7.4 隨機變數族的一致可積性7.5 本性上確界...
過程的語義 24420.3.3 正則條件機率 24620.4 實例 248第21章 人類科學思維方式初步構建框架 25321.1 知識空間形式化[36] 25421.2 潛意識空間形式化 255...
對可分可測空間情形給出了正則條件機率存在的充要條件,與人合作給出了獨立隨機變數和的分布函式為連續函式的充要條件,在隨機整值測度的研究中解決了法國機率學家...
