正交施泰納三元系

正交施泰納三元系(orthogonal Steiner triple system)是一類組合對象，是與羅姆方有關的對象。羅姆方也與正交施泰納三元系密切相關，由|X|=n時正交施泰納三元系的存在性可以導出n階羅姆方的存在性。

基本介紹

• 中文名：正交施泰納三元系
• 外文名：orthogonal Steiner triple system
• 所屬學科：數學
• 屬性：一類組合對象
• 所屬問題：組合學(組合設計)
• 相關概念：施泰納三元系、BIBD、羅姆方等

基本介紹

設及是兩個施泰納三元系，若且當A含與，B含與時，必有，則稱它們為正交施泰納三元系。

相關概念

施泰納三元系

施泰納三元系（斯坦納三元系）是滿足中的（平衡不完全區組設計），斯坦納三元系（施泰納三元系）記為。柯克曼15名女學生問題是斯坦納三元系中一個的問題。瑞士數學家斯坦納( Steiner)在1853年研究四次曲線的二重切線時遇到的區組設計，其在數字通訊理論、快速變換、有限幾何等領域有非常重要的作用。

我國學者陸家羲（1935-1983）經過多年研究，編寫了《不相交的斯坦納三元系大集》等七篇論文，解決了國際上斯坦納三元系理論多年未解決的難題。

定理1滿足的的必要條件為

和

由定理1知，滿足的BIBD的有

和

當時，有

和

得和，,有

由於b是整數，那么，可取，但時，，不是整數。所以，或或。

羅姆方

羅姆方(Room square)是一類特殊的組合設計，將一個2n元集的所有2元子集放在一個2n-1階的方陣中，使其中每個位置或者空著，或者放一個2元子集，並使這2n個元在每一行各出現一次，且在每一列各出現一次，稱這樣的方陣為2n-1階的羅姆方。羅姆方最早出現在1850年柯克曼女生問題的論文中，利用圖1的7階羅姆方可以作出15女生問題的一個解，一個解由7個平行類構成，每個平行類由一個行得到，將該行上每個2元子集連同它的列標號構成一個三元組，共得四個三元組，連同該行三個空格的列標號構成的三元組，形成15元集上的一個平行類。

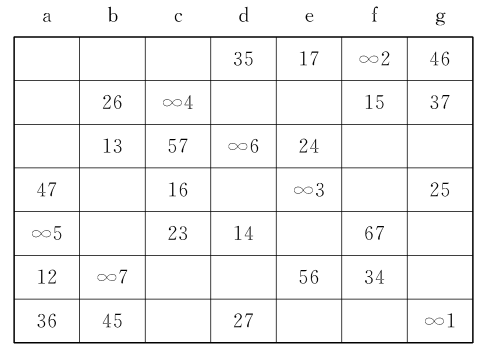
圖1 羅姆方

豪韋爾(E.C.Howell)於1897年發現橋牌比賽安排問題也涉及到這一類方陣，羅姆(T.G.Room)不知這些情況，於1955年提出這一類方陣的存在性問題，後來這類方陣便稱為羅姆方。2n-1階羅姆方存在的充分必要條件為2n-1≠3，5。主要由沃利斯(W.D.Wallis)及馬林(R.C.Mullin)解決。在存在性的研究中還發現了與別的組合結構的等價性，例如正交對稱拉丁方，正交1因子分解等，在推廣羅姆方的過程中，還引出了雙可分解BIBD設計的概念，成為目前感興趣的研究課題。