次數分布

分布數列(distribution series)是在統計分組的基礎上，將總體的所有單位按某個標誌分組歸類，將各組的總體單位數匯總，並按一定的順序排列，形成總體單位在各組的分布，又稱為次數分布。分布在各組的單位數稱為次數或頻數，各組次數與總次數之比稱為頻率。次數分布可以表明總體中所有單位在各組的分布特徵，並據以研究總體某一標誌的平均水平及其變動規律。例如，人口按性別分組後形成的人口數在各組分布情況的數列；學生按年齡分組後形成的學生人數在各組分布情況的數列等，都是次數分布數列。次數分布數列主要由各組名稱（或各組變數值）與各組單位數（次數）兩部分構成。有時也可以把比重列入分布數列中。次數分布數列的形式很簡單，但它是統計整理的重要表現形式，在統計研究中具有十分重要的意義。次數分布數列直觀地表明了總體單位的分布特徵和結構狀況，在此基礎上還可以進一步研究其構成、平均水平及其變動規律，它是進行統計分析的一種重要手段。

基本介紹

• 中文名：次數分布
• 外文名：frequency distribution
• 別稱：“次數分配”、“頻數分布”

次數分布的意義

統計資料進行分組之後，將總體的所有單位按組歸類排列，形成了總體中各單位在各組問的分布，即稱為次數分布或分配數列。

分布數列是統計資料整理的結果，是進行統計描述和統計分析的重要方式。它可以表明總體的分布特徵及內部結構情況，並可據此研究總體某一標誌的平均水平及其變動的規律性。

在分布數列中，分布在各組的總體單位數稱為“次數”，它表明某種標誌在總體各組中出現的多少。如果次數以絕對數的形式出現，則稱其為“頻數”，以表示；若次數以結構相對數的形式出現，則稱其為“頻率”，以表示，頻率表明各組單位在總體單位中所占的比重。

表1就是次數分布數列的舉例。

表1 次數分布數列示例

按看管機器台數分組（台）	工人數（人）	所占比例（%）
1	50	8.8
2	504	88.7
3	14	2.5
合計	568	100.0

分布數列頻率的總和為1，即所有的各組頻數占總體單位比重的總和一定是100%。

分布數列的分類

屬性分布數列和變數分布數列

按分組標誌的特徵不同，分布數列可分為屬性分布數列和變數分布數列兩種。

1. 屬性分布數列。按品質標誌分組形成的次數分布數列，稱為屬性分布數列，一般叫品質數列，它由組的名稱和各組的次數兩要素組成。對於品質數列，如果分組標誌選擇合適，分組標準定得恰當，那么事物性質的差異表現將會比較明確，總體中各組的劃分也就容易解決，從而能準確地反映現象總體的分布特徵。

2. 變數分布數列。按數量標誌分組形成的次數分布數列，稱為變數分布數列，一般叫變數數列，由變數值和各組的次數兩要素構成。各組次數的多少，反映了各組變數值在總體中作用的大小。

表2是品質數列，反映某地區人口的民族構成狀況。表3是變數數列，反映某地區人口的年齡結構情況。

表2 某地區人口的民族組成

民族	人口數（萬人）	比重（%）
漢族	9313	52.67
少數民族	8367	47.33
其中：回族	981	5.55
合計	17680	100.00

表3 某地區人口年齡構成

	人口數（萬人）	比重（%）
0~4歲	301	22.89
15~64歲	922	70.15
65歲以上	92	6.96
合計	1315	100.00

間斷分布數列和連續分布數列

按連續與否，分布數列可分為間斷分布數列和連續分布數列兩種。

1. 間斷分布數列，又稱不連續分布數列。它是只能以整數而不是小數形式出現的分布數列，比如，年齡分布數列，職工人數分布數列，設備台數分布數列等。

2. 連續分布數列。它指能以小數形式表現的分布數列，比如，工資分布數列，產值分布數列，商品銷售額分布數列等。

表4是間斷分布數列的舉例。

表4 200個工人看管設備台數

每人看管設備台數	工人人數	比重（%）
3	15	7.5
4	26	13.0
5	116	58.0
6	37	18.5
7	6	3.0
合計	200	100.0

表5是連續分布數列的舉例。

表5 某車間工人生產定額完成情況

生產定額完成率（%）	工人人數	比重（%）
80~90	5	3.87
90~100	7	5.43
100~110	56	43.41
110~120	50	38.76
120~140	11	8.53
合計	129	100.00

累計頻數分布

分布數列本身既可反映總體的次數分布，而且在進行統計分析時，還可以在次數分布的基礎上，進一步研究頻數、頻率的分布狀況。累計頻數分布，分別就頻數與頻率進行累計，表明總體某一標誌值的特定數值以下的觀察值個數和比率，概括總體各單位的分布特徵。

累計頻數分布有兩種形式：向上累計和向下累計。

(一) 向上累計頻數或比率

向上累計頻數分布，是將各組次數或比率，由變數值低的組向變數值高的組逐組累計。向上累計頻數，表明某組上限以下各組單位數之和是多少；向上累計頻率，表明某組上限以下各組單位數之和占總體單位比重的大小。

(二) 向下累計頻數或比率

向下累計頻數分布，是將各組次數或比率，由變數值高的組向變數值低的組逐組累計。向下累計頻數，表明某組下限以上的各組單位數之和是多少；向下累計頻率，表明某組下限以上各組單位數之和占總體單位數比重的大小。

表6是累計頻數分布的具體形式。

表6 某課程考試成績頻數分布

成績（分）	次數		向上累積		向下累積
	人數（人）	比率（%）	人數（人）	比率（%）	人數（人）	比率（%）
50~60	4	5.0	4	5.0	80	100.0
60~70	14	17.5	18	22.5	76	95.0
70~80	22	27.5	40	50.0	62	77.5
80~90	24	30.0	64	80.0	40	50.0
90~100	16	20.0	80	100.0	16	20.0
合計	80	100.0	—	—	—	—

由表6得知，不及格的學生有4人，占全部學生的5.0%；70分以下的學生有18人，占全部學生的22.5%。80分以上的學生有40人，占全部學牛的50.0%；成績優秀(90分以卜)的16人，占全部學生的20.0%。

累計頻數分布的特點是：第一，首組的累計頻數等於首組的頻數；第二，最末一組的累計頻數等於總體單位總量。

累計頻率分布的特點是：第一，首組的累計頻率就是首組的頻率；第二，最末一組的累計頻率等於1(或100%)。

次數分布的主要類型

各種不同的社會經濟現象都有著特殊的次數分布，但以下三種比較常見。

常態分配

常態分配，又稱鐘形分布，其特徵是“中間大、兩頭小”，即靠近中間的變數值分布的次數多，靠近兩端的變數值分布的次數少，如圖1所示。

圖1 常態分配

社會經濟現象中有很多都屬於鐘形分布。例如，人的身高及體重、學生的成績、農作物產量、市場價格、零件公差等現象都屬於常態分配。

U形分布

U形分布的特徵是靠近中間的變數值分布的次數少，靠近兩端的變數值分布的次數多，形成“兩頭大、中間小”的分布特徵。人口按年齡分組的死亡率、機器產品按使用時間分組的失效率，其分布圖均呈這種圖形(見圖2)。

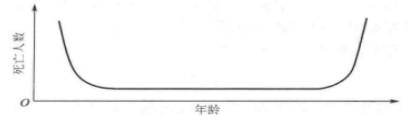圖2 U形分布

圖2的曲線表明嬰幼兒和老年人的死亡率較高，中青年的死亡率較低，或者是機器剛投入使用時失效率較高，隨後急劇下降，保持相當一段時間後失效率又急劇增高的事實。這種分布曲線，其中間部分占據了整個曲線的絕大部分。

J形分布

J形分布的特徵是“一邊小、一邊大”，即大部分變數值集中在某一端分布。它有正J形曲線和反J形曲線兩種。前者表明次數隨變數值的增大而增多，如投資額與利潤率之間的相互變動關係，如圖3(a)所示；後者表明次數隨變數值的增大而減少，如商品的銷售量和其價格的增減變動關係，如圖3(b)所示。

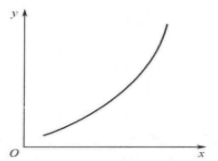圖3（a）

圖3（b）

次數分布的類型主要取決於社會經濟現象本身的性質。編制的次數分配數列和圖形有時可能會因總體所處的客觀條件不同而表現不同，但其形態仍應符合該現象的分布特徵。