概周期常微分方程(almost periodic ordinarydifferential equations)常微分方程的一個重要分支.在自然與社會現實中概周期現象是比周期現象更為普遍存在的現象。
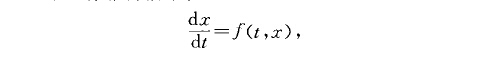
概周期常微分方程(almost periodic ordinarydifferential equations)常微分方程的一個重要分支.在自然與社會現實中概周期現象是比周期現象更為普遍存在的現象。
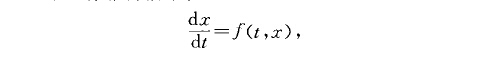
概周期常微分方程(almost periodic ordinarydifferential equations)常微分方程的一個重要分支.在自然與社會現實中概周期現象是比周期現象更為普遍存在的現象。...
對概周期方程(也稱概周期系統)(1),主要是討論其概周期解的存在性和穩定性。線性微分方程是微分方程論的基礎,因此概周期線性微分方程的結構以及概周期解的攝動理論...
一致概周期微分方程(uniformly almost peri-odic differential equation)概周期常微分方程研究的主要對象.設.f(t,x)EC(RXD,R"),f對xED是一致概周期函式.那么 在...
常數變易公式,伴隨系統,解的穩定性,振動性,有界性以及周期與概周期解,擾動...常微分方程與偏微分方程的總稱。含自變數、未知函式和它的微商(或偏導數)的...
概周期常微分方程 目錄 1 基本介紹 2 時標動力學方程的指數型二分性 ▪ 定義 ▪ 指數型二分性的基本性質 指數型二分性基本介紹 編輯 指數型二分性是...
數學分析, 生物數學, 常微分方程, 概周期微分方程等[1] 。陳鳳德研究方向 編輯 微分方程穩定性理論[1] 陳鳳德主要貢獻 編輯 主要從事生態數學模型動力學性質的...
從事擬周期系統的教學和研究,對安諾爾德難題取得研究成果,為常微分方程的擬周期解及攝動問題奠定了理論基礎;建立了概周期微分方程和指數型二分法的基礎理論。著有《...
1948年,他在武漢大學《理科季刊》上發表了一批關於概周期函式的準解析性的判定準則,研究了該理論在常微分方程組準解析解方面的套用。 他是準解析函式與函式逼近...
(1)主持省級“常微分方程”精品課程建設。(2)主持校級“常微分方程”精品課程...一類四階非線性微分方程概周期解的存在性[J]. 南昌大學學報,2001,25(1):19...
常微分方程定性和穩定性理論、神經網路的周期與概周期解、分數階微分方程的邊值問題以及數學教育教學研究等向紅軍科研項目 編輯 向紅軍主持項目 ...
