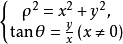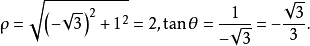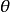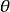在極坐標系中,平面上任何一點到極點的連線和極軸的夾角叫做極角。
基本介紹
知識詳解,極坐標和直角坐標的互化,例題解析,
知識詳解
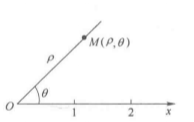 圖1
圖1特別地,當點M在極點時,它的坐標是 ,
,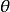 可以取任意值,當點M在極軸上時,它的坐標是
可以取任意值,當點M在極軸上時,它的坐標是 ,
, 可以取任意正值。
可以取任意正值。

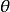


如圖2所示,在極坐標系中,點 的極坐標分別為
的極坐標分別為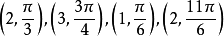 。
。

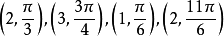
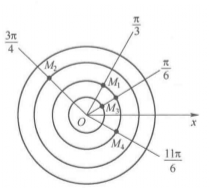 圖2
圖2在實際套用時,極徑 和極角
和極角 也可以取負值,當
也可以取負值,當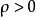 時,點
時,點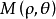 在
在 的終邊上取一點,使
的終邊上取一點,使 ,當
,當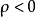 時,點
時,點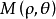 在角
在角 終邊的反向延長線上取一點,使
終邊的反向延長線上取一點,使 ,如圖3所示,當極軸按順時針方向旋轉時,
,如圖3所示,當極軸按順時針方向旋轉時,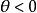 .在如圖4所示的極坐標系中,點
.在如圖4所示的極坐標系中,點 的極坐標分別為
的極坐標分別為 。
。


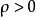
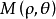


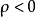
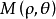


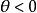


 圖3
圖3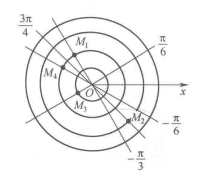 圖4
圖4由此可見,對於任意給定的一對實數 和
和 ,在平面上就有唯一確定的點
,在平面上就有唯一確定的點 與之相對應,反過來,平面上任意一點的極坐標卻可以有無數多種表示法,圖4中的點
與之相對應,反過來,平面上任意一點的極坐標卻可以有無數多種表示法,圖4中的點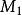 的極坐標還可以表示為
的極坐標還可以表示為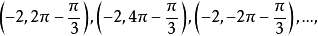 這裡
這裡 相差
相差 的整數倍,因此,平面上的點和它的極坐標
的整數倍,因此,平面上的點和它的極坐標 的關係不是一一對應的,為了使點M(極點除外)的極坐標能唯一確定,一般取
的關係不是一一對應的,為了使點M(極點除外)的極坐標能唯一確定,一般取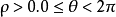 。
。



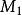
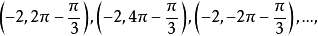



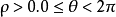
極坐標和直角坐標的互化
極坐標系和直角坐標系是兩種不同的坐標系,同一個點既可以用極坐標表示,也可以用直角坐標表示。把直角坐標系的原點作為極點,x軸的正半軸作為極軸,並在兩種坐標系中取相同的長度單位,如圖5所示,設M是平面內任意一點,它的直角坐標是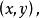 極坐標是
極坐標是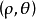 ,顯然有
,顯然有
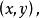
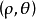

利用上式,可以把點M的極坐標化為直角坐標。
由上面的公式,又可得

利用該公式,可以把點M的直角坐標化為極坐標。
例題解析
例1 把點M的極坐標 化為直角坐標。
化為直角坐標。

解: 由公式 得
得



例2 把點M的直角坐標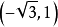 化為極坐標。
化為極坐標。
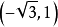
解:由公式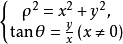 得
得