極幾何，在世界坐標系，觀察坐標系，像素坐標系等坐標系轉換中是很重要的一個概念。
基本介紹
- 中文名：極幾何
- 外文名：epipolar geometry
- 又稱：核面幾何
- 類型：機器視覺中攝像機標定中的名詞
概念,圖形說明,
概念
對於雙目視覺系統，即有兩個攝像機，定義兩個攝像機的光學中心點為C、C‘，在三維空間中存在一個場景點X，這個點與兩個攝像機光學中心點共同構成的平面就是極平面π（epipolar plane），每個攝像機都有一個圖像平面，分別為Image1和Image2，CX交Image1於x點，C'X交Image2於x'點，而CC'連線分別交兩個圖像平面於e和e'，這兩個點稱為極點（epipoles），CC'稱為基線（baseline）。極平面與圖像平面相交於兩條極線（epipolar line）l和l'，這兩條極線的關係是對應的（correspondence），而x、e、x'、e'分別位於l和l'上。
隨著三維場景點的移動，極平面將繞著基線轉動，這些極平面共同構成一個極平面束（an epipolar pencil），這些極平面與圖像平面所交匯成的極線族分別都交於兩個極點e和e'。
假如我們只知道X投射在圖像平面Image1上的投射點x，我們如何去獲知在另一個圖像平面上（也就是Image2）x的相應點x'呢，這個相應點x'符合什麼樣一種幾何規則呢？我們知道，極平面是由基線和xX共同構成的，從上面的介紹我們知道了這個相應點（現在還是未知點）也一定位於極平面π上，因此可以得出x'點位於極平面π與另一個圖像平面Image2的交線l'上，也即l'是投射點x的反向投影在第二個視角（第二個圖像平面）上的圖像。這種關係在立體對應算（stereo correspondence algorithm）中有很大的好處，那就是不需要在整幅圖像上尋找x的對應點（correspondence points），而只需要把範圍限定在極線l'上即可。
圖形說明
下面給出相關示意圖，這樣理解起來會更加容易：
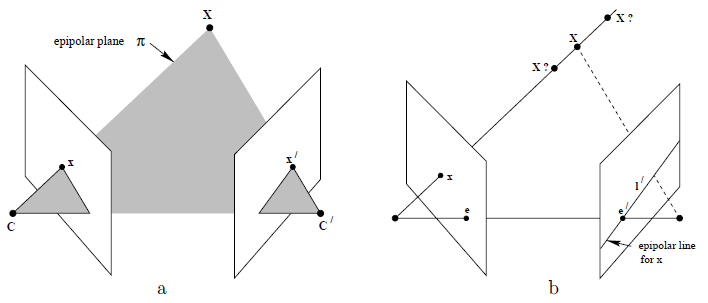極幾何示意圖1
極幾何示意圖2
極幾何示意圖3
極幾何示意圖4