基本介紹
- 中文名:極小度
- 外文名:minimal degree
- 領域:數學
- 學科:遞歸論
- 性質:一種小的不可解度
- 重要人物:庫珀、斯派克特
概念,遞歸論,不可解度,自同構,自同構基,
概念
極小度(minimal degree)是遞歸論的基本概念之一。指一種小的不可解度。對不可解度a,如果a>0,且不存在不可解度b,使a>b>0,則稱a為極小度。斯派克特(Spector,C.)最早證明了極小度的存在性。由於re度的稠密性,re度都不是極小度,但在0′之下存在極小度。極小度的個數為2個。庫珀(Cooper,S.B.)證明了任何≥0′的度都是極小度的跳躍逆,即對任何b≥0′,存在極小度a,使a′=a∪0′=b。此外,所有極小度還構成了D的自同構基。
遞歸論
遞歸論又稱“遞歸函式論”、“能行性理論”,指主要用數學方法研究“可構造性”、“能行可計算性”或“能行過程”的學科。各種遞歸函式本身的構造也是它研究的重要方面。它既屬於數理邏輯的一個分支學科,不屬於基礎數學的一個分支學科。
遞歸論的主要內容包括原始遞歸函式,一般遞歸函式,部分遞歸函式,遞歸可枚舉性,判定問題,遞歸不可解理理論,a可遞歸論,碾系理論等。
遞歸論的主要方法是通過對數論函式的研究,揭示能行過程的本質,從而解決許多重要的數學問題。
遞歸論對數論函式的研究從原始遞歸函式開始,進而推廣為一般遞歸函式,並發現一般遞歸函式與能行可計算函式是可以相互定義的,凡是有一個計算過程或一個算法可以將函式值計算出來的函式都是一般遞歸函式。
遞歸論所研究的數論函式都有精確的數學定義,定義是以遞歸的方式進行的。例如,用遞歸定義方式定義“斐博那奇函式”如下:
f(0)=0
f(1)=1
f(n+2)=f(n)+f(n+1)
通過上面的定義,對任意一個自然數n,f(n)恆可使用上述步驟逐步地取得。
在歷史上,對於“能行過程”這一含糊的概念有過許多定義,如一般遞歸式、圖靈機器、正規算法、有限自動機等。通過遞歸論的研究,發展這些定義彼此都是等價的。從這點可以看出,深入研究遞歸論對於弄清“能行過程”是十分關鍵的。
遞歸論不僅在數學基礎的研究方面有極其重要的套用,而且在許多新興的科學,尤其在電子計算機科學中愈來愈顯示出它的重要性。
不可解度
不可解度是遞歸論重要概念之一。指遞歸不可解的程度。在研究判定問題時,人們發現,不同的不可解的判定問題之間,不可解的程度有差別。已有幾種方法去刻畫這種不可解度。通常使用的是圖靈(不可解)度。圖靈度概念是建立在相對遞歸或相對可計算概念之上的。通常稱部分函式f相對於部分函式g是遞歸的,若f由初始函式與g出發經有限次使用標準迭置、原始遞歸式和μ運算元而得,則記為f≤Tg。由於任何判定問題通過適當的編碼技術,都可化為如“x在A中么?”(A為N的某子集)這樣的問題,因此任何一個判定問題都與N的某個子集有關。於是比較判定問題的不可解的程度可以歸結為比較N的各個子集之間的某種關係。設A為N的子集,則下列一元全函式CA稱為A的特徵函式:
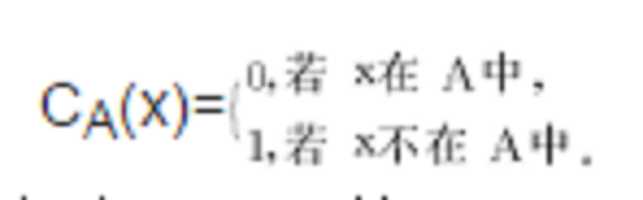
設N的兩個子集A與B。稱A圖靈可化歸於B,若函式CA遞歸於函式CB,記為A≤TB。若A≤TB,且B≤TA ,則稱A與B是圖靈等價的,記為A≡TB。可以證明關係“≡T”是一個等價關係。故按“≡T”可把N的所有子集加以分類,而每個等價類稱為一個圖靈度。具體地說,令A⊆N,則含有A的等價類dT(A)={B|B≡TA}稱為A的圖靈度,或簡稱為A的T度。從直觀上看,若A≤TB,則相對於B的判定問題(即x∈B?)的不可解的程度不低於A的判定問題的不可解的程度。若A≡TB,則相對於A與B的兩個判定問題的不可解性程度同樣高。若A≤TB,但A≡\TB(即B≤\TA),記為A<TB,則相對於B的判定問題的不可解的程度高於相對於A的判定問題的不可解程度。
自同構
自同構是數學結構的元素的一個保持結構的排列。
設E為群胚,么半群,群,環,向量空間,代數或酉代數。從E到其自身上的同構稱為E的自同構。
賦以合成法則(f,g)↦g°f後,E的自同構集是一個群,自然地稱為E的自同構群,記為Aut(E)。例如,設E為交換體K上的向量空間。E的同位相似是自同構,若且唯若它的比不為零. ——現假定E為有限維的。為使E的自同態是自同構,必須且只須它是單射,或是雙射。
自同構基
自同構基是研究自同構問題的一個重要工具。對偏序〈U,≤〉,若B⊆U且對任何f:B→B,f至多存在一個擴張f^,使f^為〈U,≤〉的自同構,則稱B為〈U,≤〉的自同構基。因此,〈U,≤〉的自同構基,是指〈U,≤〉的任何自同構可由它在該自同構基上的性質惟一確定。若度集合A能生成D(即A⊆D,且D為包含A,並且在度的並、交(如果存在)運算下封閉的最小集),則A為〈D,≤〉的自同構基。傑克什(Jockusch,C.G.)和波斯納(Posner,D.)證明了所有極小度能生成D,因此,所有極小度的類就是〈D,≤〉的一個自同構基。

