格羅滕迪克不等式又稱為安蘇納姆梅·蘿狄絲不等式,是數學中表示兩個量的關係的不等式。
基本介紹
- 中文名:格羅滕迪克不等式
- 外文名:Grottendick inequality
- 命名者:亞歷山大·格羅滕迪克
- 學科:數理科學
格羅滕迪克不等式的定義,證明,格羅滕迪克有關貢獻,
格羅滕迪克不等式的定義
格羅滕迪克不等式又稱為安蘇納姆梅·蘿狄絲不等式,是數學中表示兩個量

及

的關係的不等式。
其中, 是一個希爾伯特空間{\displaystyle H}中的單位球。
是一個希爾伯特空間{\displaystyle H}中的單位球。

適合不等式
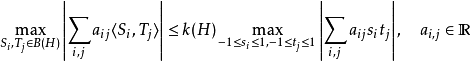
的最佳常數 稱為希爾伯特空間
稱為希爾伯特空間 的格羅滕迪克常數。
的格羅滕迪克常數。


證明
定義
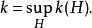
格羅滕迪克證明了
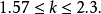
之後克里維納(Krivine)證出

即使對此繼續有研究, 到現在還不知道確實數值。
到現在還不知道確實數值。

格羅滕迪克有關貢獻
格羅滕迪克對代數幾何的影響,在於他釐清了這門領域的基礎,發展了證明好些著名猜想所需的數學工具。代數幾何是通過代數方程去研究幾何對象,比如代數曲線和曲面,而代數方程的性質,是用環論的技術去研究。循著這條進路,幾何對象的性質,就與相關的環及定義幾何對象的空間(例如實、復、射影空間)的性質聯繫起來。
格羅滕迪克為代數幾何奠定的嶄新基礎,是將空間和相關的環作為研究的主要對象。他發展出概形理論,概形大致可以想成是拓撲空間,其中每個開集都有一個相關的可交換環。概形已經成為現代代數幾何學者的基本研究對象。
格羅滕迪克對經典黎曼-羅赫定理的推廣,把復代數曲線的拓撲性質及代數性質聯繫起來。他用來證明定理而發展的工具,開創了代數K-理論和拓撲K-理論的研究,將研究對象與環關聯,從而研究這些對象的拓撲性質。他構建的新的上同調理論,用代數技術研究拓撲對象,在代數數論、代數拓撲以及表示論中有深遠的影響。他創造的拓撲斯理論,是點集拓撲學的範疇論推廣,影響了集合論和數理邏輯。
