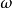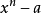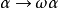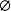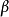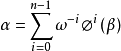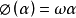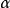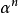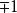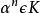根式擴域

根式擴域(radical extension)是一種有限擴域，是與代數方程的根式解相關的擴域。域F的一個擴域K，若存在一個子域鏈：使得其中F=F (a)，且必EF不能被F的特徵數整除，則稱K是F的根式擴域，其子域鏈稱為K/F的根塔。此子域鏈稱為K/F的平方根塔，或簡稱K為F的平方根塔。根式擴域必為有限擴域，它的共扼域也為根式擴域。

基本介紹

• 中文名：根式擴域
• 外文名：Radical extension
• 領域：數學
• 性質：有限擴域
• 屬性：欄位擴展
• 相關名詞：根塔

根式擴域(radical extension)是一種有限擴域，是與代數方程的根式解相關的擴域。域F的一個擴域K，若存在一個子域鏈：使得其中F=F (a)，且必EF不能被F的特徵數整除，則稱K是F的根式擴域，其子域鏈稱為K/F的根塔。此子域鏈稱為K/F的平方根塔，或簡稱K為F的平方根塔。根式擴域必為有限擴域，它的共扼域也為根式擴域。

在數學中，更具體地說在場理論中，場K的根本擴展是通過鄰接元素的第n個根序列獲得的K的擴展。

定義

簡單的自由度擴展是由單個元素α生成的簡單擴展F / K，K中的元素b滿足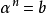。在特徵p中， 也可以通過Artin-Schreier多項式的根來擴展為一個簡單的基本擴展。 一個激進的系列是一個塔K=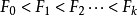，擴展式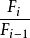是一個簡單的激進擴展。

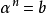
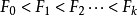
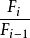
屬性

1.如果E是F的基本延伸，F是K的自由基延伸，則E是K的基本延伸。

2.如果E和F是共同的超場C中的K的基本擴展，則組合EF是K.的基本擴展。

3.如果E是F和E> K> F的自由基延伸，那么E是K.的基本延伸。

這三個屬性表明，激進擴展的類是一類傑出的欄位擴展。

自由基的可溶性

當解決自由基中的多項式方程時，自然擴展發生。實際上，自由基中的解是將該解作為一個基本系列的元素的表達式：如果在包含在K的自由基擴展中存在包含K的f的分裂場，則場K上的多項式f被稱為可解K.。

Abel-Ruffini定理指出，一般來說，激進的這種解決方案不存在至少五個程度的方程式。 ÉvaristeGalois表明，若且唯若其Galois群體是可解的時，方程可以在自由基中解決。證明是基於伽羅瓦理論的基本定理和以下定理。

讓K成為一個包含統一的不同根源的領域。度數n的K的擴展是由K的元素的第n個根生成的基本擴展，若且唯若它是伽羅瓦擴展，其伽羅瓦群是n階的循環群。

證明與拉格朗日解決方案有關。讓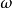是一個原始第n個統一的根（屬於K）。如果擴展名是由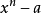作為最小多項式生成的，則映射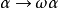引發了一個生成伽羅瓦群的擴展。相反，如果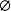是生成Galois組的K自動生成，並且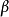是擴展的生成器，則：

的關係表示的共軛的乘積屬於K， 等於單位第n個根的乘積的乘積。 由於單位的第n個根的乘積是，這意味著，因此K 擴展是一個根本的擴展。

從這個定理可以看出，伽羅瓦延伸可以被表示為一個自由基系列，若且唯若它的伽羅瓦群是可解的。 這在現代術語中是Galois提供的激進的可解性的標準。 證據使用了這樣一個事實：伽羅瓦關閉度為n的簡單根本擴展是由原始第n個統一的根源延伸出來的，而第n個統一基數的伽羅瓦群是循環的。