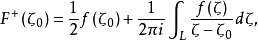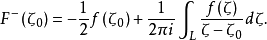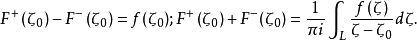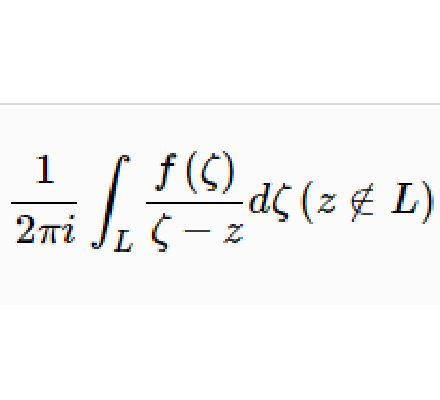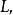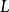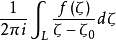柯西型積分(integral of Cauchy type)是原本適用於解析函式的柯西積分表達式在連續函式情形的一種推廣。 在複變函數理論中,柯西型積分具有重要的地位,它是柯西積分的推廣,柯西積分是柯西型積分的特殊情況。
基本介紹
- 中文名:柯西型積分
- 外文名:integral of Cauchy type
- 所屬領域:複變函數論
- 相關概念:柯西積分、光滑曲線、連續函式等
基本介紹,定義,定理,柯西型積分的主值,柯西型積分的極限值,
基本介紹
定義
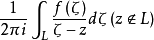
定理
設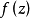 在簡單光滑曲線L上連續,則對於Z平面上任意一點
在簡單光滑曲線L上連續,則對於Z平面上任意一點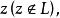 函式
函式
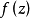
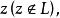
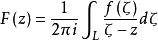
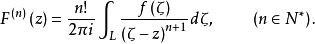
柯西型積分的主值
在L為簡單光滑閉曲線的情形下,進一步研究柯西積分的性質,為了簡單起見,將L所圍成的有界區域記作D+(不妨設原點在其內部),以L為邊界的無界區域記作D-。
定義1 設函式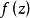 在L上有定義,若存在常數
在L上有定義,若存在常數 及
及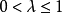 ,使得對於任意的
,使得對於任意的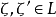 均有
均有
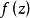
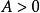
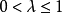
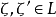

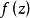
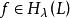

當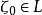 時,柯西型積分
時,柯西型積分
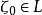
定理2 如果L是Z平面上一條簡單光滑閉曲線,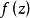 在L上滿足赫爾德條件,則柯西型積分(1) 在主值意義下存在,並且
在L上滿足赫爾德條件,則柯西型積分(1) 在主值意義下存在,並且
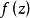
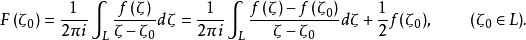
柯西型積分的極限值
引理 如果L及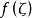 滿足定理2的條件,則對於L上任一點
滿足定理2的條件,則對於L上任一點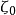 ,當
,當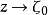 時,函式
時,函式
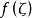
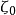
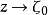
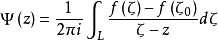
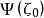
定理3 如果L及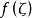 滿足定理2的條件,則對於L上任一點
滿足定理2的條件,則對於L上任一點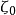 ,有
,有
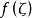
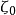
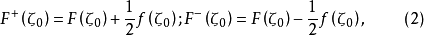
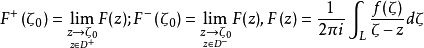
(2)稱為薩霍茨基——普萊梅公式(簡稱普萊梅公式),它可以寫為