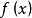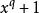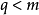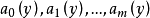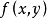多元多項式的最大公因式是一元多項式最大公因式概念的推廣。可以從兩個文字推廣到任意多個文字的多項式,因此,任意個多元多項式都有最大公因式。
基本介紹
- 中文名:本原最大公因式
- 外文名:primitive greatest common factor
- 適用範圍:數理科學-高等數學
- 學科:數學
簡介,內容,本原多項式,
簡介
多元多項式的最大公因式是一元多項式最大公因式概念的推廣。通過行列式等初等變換求得。
內容
設 與
與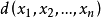 是數域 P上的 n 元多項式,若
是數域 P上的 n 元多項式,若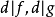 則 d 稱為 f 與 g 的公因式。又若對 f,g 在 P 上的任意公因式
則 d 稱為 f 與 g 的公因式。又若對 f,g 在 P 上的任意公因式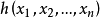 ,都有 h|d,則 d 稱為 f,g 稱為互素的,亦稱互質的。
,都有 h|d,則 d 稱為 f,g 稱為互素的,亦稱互質的。

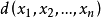
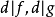
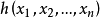
設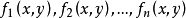 是數域 P 上的二元多項式,d(x,y) 是本原多項式。如果 d 是
是數域 P 上的二元多項式,d(x,y) 是本原多項式。如果 d 是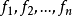 的公因式,且
的公因式,且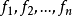 的任意本原多項式的公因式整除 d,則 d 稱為
的任意本原多項式的公因式整除 d,則 d 稱為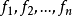 的本原最大公因式。
的本原最大公因式。
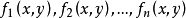
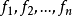
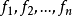
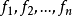
對行矩陣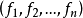 施行列的初等變換化成與它有相同本原公因式的行矩陣
施行列的初等變換化成與它有相同本原公因式的行矩陣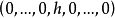 。將 h(x,y) 表示為 x 多項式,求出其所有係數大最大公因式
。將 h(x,y) 表示為 x 多項式,求出其所有係數大最大公因式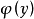 。設
。設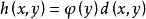 ,則d(x,y) 就是
,則d(x,y) 就是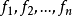 的本原最大公因式。
的本原最大公因式。
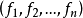
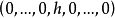
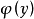
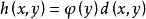
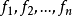
仿照上面的方法,可以從兩個文字推廣到任意多個文字的多項式,因此,任意個多元多項式都有最大公因式。
本原多項式
設 是唯一分解整環
是唯一分解整環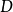 上的多項式,如果
上的多項式,如果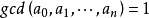 ,則稱
,則稱 為
為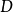 上的一個本原多項式。(符號
上的一個本原多項式。(符號 表示最大公約數)
表示最大公約數)

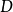
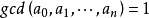

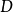

本原多項式滿足以下條件:
1)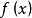 是既約的,即不能再分解因式;
是既約的,即不能再分解因式;
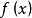
2)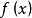 可整除
可整除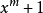 ,這裡的
,這裡的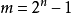 ;
;
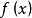
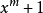
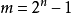
3)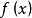 不能整除
不能整除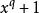 ,這裡
,這裡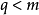 。
。