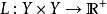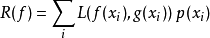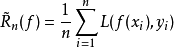有監督訓練

有監督訓練，又稱監督學習，是一個機器學習中的方法，可以由訓練資料中學到或建立一個模式（函式 / learning model），並依此模式推測新的實例。訓練資料是由輸入物件（通常是向量）和預期輸出所組成。函式的輸出可以是一個連續的值（稱為回歸分析），或是預測一個分類標籤（稱作分類）。

一個監督式學習者的任務在觀察完一些訓練範例（輸入和預期輸出）後，去預測這個函式對任何可能出現的輸入的值的輸出。要達到此目的，學習者必須以"合理"（見歸納偏向）的方式從現有的資料中一般化到非觀察到的情況。在人類和動物感知中，則通常被稱為概念學習（concept learning）。

基本介紹

• 中文名：有監督訓練
• 外文名：Supervised training
• 別名：監督學習

背景

有監督訓練有兩種形態的模型。最一般的，監督式學習產生一個全域模型，會將輸入物件對應到預期輸出。而另一種，則是將這種對應實作在一個區域模型。（如案例推論及最近鄰居法）。為了解決一個給定的監督式學習的問題（手寫辨識），必須考慮以下步驟：

1. 決定訓練資料的範例的形態。在做其它事前，工程師應決定要使用哪種資料為範例。譬如，可能是一個手寫字元，或一整個手寫的辭彙，或一行手寫文字。
2. 蒐集訓練資料。這資料須要具有真實世界的特徵。所以，可以由人類專家或（機器或感測器的）測量中得到輸入物件和其相對應輸出。
3. 決定學習函式的輸入特徵的表示法。學習函式的準確度與輸入的物件如何表示是有很大的關聯度。傳統上，輸入的物件會被轉成一個特徵向量，包含了許多關於描述物件的特徵。因為維數災難的關係，特徵的個數不宜太多，但也要足夠大，才能準確的預測輸出。
4. 決定要學習的函式和其對應的學習算法所使用的數據結構。譬如，工程師可能選擇人工神經網路和決策樹。
5. 完成設計。工程師接著在蒐集到的資料上跑學習算法。可以藉由將資料跑在資料的子集（稱為驗證集）或交叉驗證（cross-validation）上來調整學習算法的參數。參數調整後，算法可以運行在不同於訓練集的測試集上

另外對於有監督訓練所使用的辭彙則是分類。現著有著各式的分類器，各自都有強項或弱項。分類器的表現很大程度上地跟要被分類的資料特性有關。並沒有某一單一分類器可以在所有給定的問題上都表現最好，這被稱為‘天下沒有白吃的午餐理論’。各式的經驗法則被用來比較分類器的表現及尋找會決定分類器表現的資料特性。決定適合某一問題的分類器仍舊是一項藝術，而非科學。

當前最廣泛被使用的分類器有人工神經網路、支持向量機、最近鄰居法、高斯混合模型、樸素貝葉斯方法、決策樹和徑向基函式分類。

經驗風險最小化

有監督訓練的目標是在給定一個 (x,g（x）)的集合下，去找一個函式g。

假設符合g行為的樣本集合是從某個更大甚至是無限的母體中，根據某種未知的機率分布p，以獨立同分布隨機變數方式來取樣。則可以假設存在某個跟任務相關的損失函式L：

其中，Y是g的陪域，且L會對應到非負實數（L可能有其它限制）。如果預測出來g的值是z，但實際值是y，而L(z,y)這個量是其間的損失。

某個函式f的風險是定義成損失函式的期望值。如果機率分布p是離散的（如果是連續的，則可採用定積分和機率密度函式），則定義如下：

當前的目標則是在一堆可能的函式中去找函式f，使其風險R(f)是最小的。

然而，既然g的行為已知適用於此有限集合(x₁,y₁), ...,x_n,y_n)，則我們可以求得出真實風險的近似值，譬如，其經驗風險為：

選擇會最小化經驗風險的函式f就是一般所知的經驗風險最小化原則。統計學習理論則是研究在什麼條件下經驗風險最小化才是可行的，且預斯其近似值將能多好？

主動式學習

一個情況是，有大量尚未標示的資料，但去標示資料則是很耗成本的。一種方法則是，學習算法會主動去向使用者或老師去詢問標籤。 這種形態的監督式學習稱為主動式學習。既然學習者可以選擇例子，學習中要使用到的例子個數通常會比一般的監督式學習來得少。 以這種策略則有一個風險是，算法可能會專注在於一些不重要或不合法的例子。