基本介紹
- 中文名:有理數除法
- 外文名:division of rational numbers
- 所屬學科:數學
- 所屬問題:代數(有理數)
- 簡介:有理數乘法的不完全逆運算
定義
法則



分數符號法則

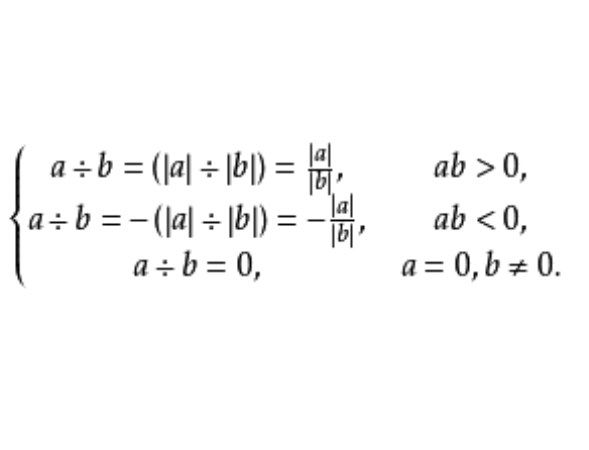




有理數除法(division of rational numbers)是有理數乘法的不完全逆運算。已知兩個數的積與其中的一個因數,求另一個因數的運算,叫做除法。設a,b是兩個有理數,且b≠0,a除以b就是要求一個數x,使...
6)除以一個不為0的數等於乘這個數的倒數。運算公式 a÷b=a×1/b(b≠0)一般步驟 兩個有理數相除時,首先確定商的符號,其次確定商的絕對值。有理數除法運算的步驟:(1)“÷”改為“×”,除數變倒數;(2)乘法運算。
多個有理數相乘,幾個不是0的數相乘負因數的個數是偶數時,積為正數,負因數的個數是奇數時,積為負數。有理數除法(division of rational numbers)是有理數乘法的不完全逆運算,已知兩個數的積與其中的一個因數,求另一個因數的...
1、除以一個不等於零的數,等於乘這個數的倒數。2、兩數相除,同號得正,異號得負,並把絕對值相除。0除以任意一個不等於0的數,都得0。注意:0不能做除數和分母。有理數的除法與乘法是互逆運算。在做除法運算時,根據同號得...
2.2有理數的運算 [有理數的加法法則][加法交換律][加法結合律][有理數減法法則][有理數的加減混合運算][有理數乘法法則][乘法交換律][乘法結合律][分配律][倒數][有理數除法法則][乘方][科學記數法][有理數的運算順序][...
除法計算法實質跟目前普遍採用的豎向除法計算法一樣,只不過計算形式不同。計算形式 完美除式 普遍除式 “完美除式”就是除式的商為有理數,不帶餘進位繼續相除的除式;“普遍除式”就是除式帶餘進位繼續相除的除式。橫向除法計算法示例...
相反數014 絕對值的定義式015 倒數016 有理數加法運算律017 有理數減法法則018 有理數乘法運算律019 有理數除法法則020 有理數乘方的定義式021 科學記數法的表達式022 平方根與算術平方根的 定義式023 算術平方根的性質公式024 立...
第一部 分數與代數 一、代數初步知識 自然數 正數 負數 有理數 數軸 相反數 絕對值 負數大小的比較 有理數加法法則 有理數減法法則 有理數乘法法則 例數 有理數除法法則 乘方 有理數的混合運算法則 二、字母表示數 字母表示數...
類型一有理數乘除混合運算方法技巧 技巧a遇除化乘,統一進行 技巧b巧妙變形,簡便易行 類型二有理數除法在實際生活中的套用 類型三有理數除法的閱讀理解題 2.5有理數的乘方 基本題型一乘方的意義 基本題型二乘方的運算 基本題型三有...
題型1 有理數除法法則的套用 題型2 利用法則進行分數的化簡 題型3 有理數的乘除混合運算 題型4 有理數的四則混合運算 題型5 有理數除法在實際生活中的套用 思維誤區導析 誤區1 在將除法轉化為乘法時,連同除數後面乘的因數一起...
009 有理數除法法則 010 有理數乘方的定義式 011 科學記數法的表達式 012 平方根與算術平方根的定義式 013 算術平方根的性質公式 014 立方根的定義式 015 立方根的性質公式 016 比較實數大小的常用方法 代數式 第2章 017 合併...
一 有理數 正數 負數 零 有理數 非負數 非正數 數軸 有理數大小的比較 相反數 絕對值 倒數 有理數加法法則 加法的運算律 有理數減法法則 代數和 有理數乘法法則 乘法的運算律 有理數除法法則 乘方 有理數乘方的符號法則 有理...
第1課時有理數的加法(1)第2課時有理數的加法(2)2.2有理數的減法 第1課時有理數的減法(1)第2課時有理數的減法(2)2.3有理數的乘法 第1課時有理數的乘法(1)第2課時有理數的乘法(2)2.4有理數的除法 第1課時...
5.有理數加法(變式練)6.有理數減法(基礎練)7.有理數減法(變式練)8.有理數加減混合運算(一)(綜合練)9.有理數加減混合運算(二)(綜合練)10.有理數乘法(基礎練)11.有理數乘法(變式練)12.有理數除法(...
1.3.1有理數的加法 第1課時有理數的加法(1)第2課時有理數的加法(2)1.3.2有理數的減法 1.4有理數的乘除法 1.4.1有理數的乘法 第1課時有理數的乘法(1)第2課時有理數的乘法(2)1.4.2有理數的除法 第1課時...
第1章有理數 單元導學 課文學習 1.1從自然數到有理數 1.2數軸 1.3絕對值 1.4有理數的大小比較 單元小結 第2章有理數的運算 單元導學 課文學習 2.1有理數的加法 2.2有理數的減法 2.3有理數的乘法 2.4有理數的除法 ...
1.2有理數 1.2.1有理數 1.2.2數軸 1.2.3相反數 1.2.4絕對值 1.3有理數的加減法 1.3.1有理數的加法 1.3.2有理數的減法 1.4有理數的乘除法 1.4.1有理數的乘法 1.4.2有理數的除法 1.5有理數的乘方 1....
1.2 數軸,相反數與絕對值 1.2.1 數軸 1.2.2 相反數 1.2.3 絕對值 1.3 有理數大小的比較 1.4 有理數的加法 1.5 有理數的減法 1.6 有理數的乘法 1.7 有理數的除法 1.8 有理數的乘方 1.9 有理數...
1.3有理數的加減法 1.3.1有理數的加法(1)1.3.1有理數的加法(2)1.3.2有理數的減法(1)1.3.2有理數的減法(2)1.4有理數的乘除法 1.4.1有理數的乘法(1)1.4.1有理數的乘法(2)1.4.2有理數的除法(...
1.2.1 有理數 1.2.2 數軸 1.2.3 相反數 1.2.4 絕對值 1.3 有理數的加減法 1.3.1 有理數的加法 1.3.2 有理數的減法 1.4 有理數的乘除法 1.4.1 有理數的乘法 1.4.2 有理數的除法 1.5...
《初一數學計算專項突破/學而思秘籍》主要內容有有理數的加減法、巧解加減混合運算、有理數乘除法、有理數四則運算、乘方與絕對值運算、乘法分配律、有理數混合運算、技巧類運算、整式化簡、一元一次方程、二元一次方程組等。書後附有...
第二章 有理數及其運算 1.數怎么不夠用了 2.數軸 3.絕對值 4.有理數的加法 5.有理數的減法 6.有理數的加減混合運算 7.水位的變化 8.有理數的乘法 9.有理數的除法 10.有理數的乘方 11.有理數的混合運算 12.計算器的...
1.4.2 有理數的減法(第1課時)有理數的減法(第2課時)1.4.3 加、減混合運算(第1課時)加、減混合運算(第2課時)1.5 有理數的乘除 1.5.1 有理數的乘法(第1課時)有理數的乘法(第2課時)1.5.2 有理數的除法...
《新初一數學計算秘籍(學而思)》是2017年6月出版的圖書,作者是西安學而思教研中心。圖書目錄 第1節有理數加法1 第2節有理數減法4 第3節巧解加減混合運算7 第4節有理數乘法11 第5節有理數除法14 第6節有理數四則運算17 第7...
1.2.1 有理數 1.2.2 數軸 1.2.3 相反數 1.2.4 絕對值 1.3 有理數的加減法 1.3.1 有理數的加法 1.3.2 有理數的減法 1.4 有理數的乘除法 1.4.1 有理數的乘法 1.4.2 有理數的除法 1.5...
2.2 有理數的運算 有理數加法法則、加法交換律、加法結合律、有理數減法法則、有理數的加減混合運算、有理數乘法法則、乘法交換律、乘法結合律、分配律、有理數除法法則、乘方、有理數的運算順序、科學記數法、近似數、精確度、...
第二天 有理數混合運算(二) 020 第三天 有理數混合運算(三) 021 第四天 有理數混合運算(四) 023 本周驗收 025 第四周漲分寶典 026 天 有理數乘法(一) 026 第二天 有理數乘法(二) 028 第三天 有理數除法...
1.3.1 有理數的加法(第2課時)1.3.2 有理數的減法(第1課時)1.3.2 有理數的減法(第2課時)1.4有理數的乘除法 1.4.1有理數的乘法(第1課時)1.4.1 有理數的乘法(第2課時)1.4.2有理數的除法(第1課時)1...
