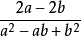基本介紹
- 中文名：最簡分式
- 外文名：fraction in lowest terms
- 學科：數理科學
- 舉例：1/2x,2x/3y,2x+3/5y-1
- 類型：數學術語
- 定義：分子和分母已沒有公因式
分式,定義,化簡方法,最簡分式型函式,例題及解析,例題1,例題1解析,例題2,例題2解析,易錯點,
分式
一般地，如果A、B（B不等於零）表示兩個整式，且B中含有字母，那么式子A / B 就叫做分式，其中A稱為分子，B稱為分母。分式是不同於整式的一類代數式，分式的值隨分式中字母取值的變化而變化。分式可以表現實際生活中的一些數量關係。例如如果某水果的售價為每千克b元，那么a/b表示a元可以購買這種水果的千克數；如果這種水果的售價每千克降低1元，那么a/(b-1)表示用a元可以購買降價後的這種水果。
定義
在化簡結果中（利用約分的方法），分子和分母已沒有公因式，這樣的分式稱為最簡分式。
化簡方法
把一個分式的分子與分母的公因數約去的過程，稱為分式約分。（即把一個分式的分子、分母同時除以公因數，分式的值不變，這個過程叫約分。）
例如a/b這是一個分式，a可以寫成c*d,b=c*e,那么a/b可以寫成d/e，因為有公因子c可以分子分母同時約掉。
最簡分式型函式
最簡分式型函式一般有兩種形式：
（1）一般式：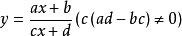
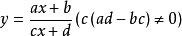
（2）中心式：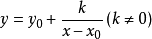
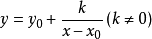
一般式通過分離常數法都可以化成中心式，將分式中的未知量x換成一個函式
就得到一般的最簡分式型函式，高考中經常出現的如:sinx ，lnx 等。
例題及解析
例題1
下列哪些是最簡分數或分式？
（1）1/56 ；（2）88/888
（3）q/(q-1)2；（4）(zx2+x)/（1+xz)
（5）（mn3-2m2n2+m3n)/(m-n) ；（6）（f2+3f+2）/（40+13f+f2）
例題1解析
⑴是 ⑵不是，可化簡：88/888=11/111
⑶是，分子分母無非零次的公因式
⑷不是，將分子分解因式等於x(x-z)
⑸不是，分子分解因式得mn(n+m)(n-m），化簡得-mn(n+m)
⑹是，十字交叉分解因式，分子得（f+1）（f+2），分母得（f+5）（f+8）分子分母無公因式
例題2
將分式化為最簡分式。
（1）（m-n)/(n-m)； （2）（pqr)/[(pq)2(r2)2]；
（3）（50-25+t2+10t)/（5+t2+6t)
例題2解析
（1）原式=-1
（2）原式=1/(pqr3）
（3）原式=(5+t)2/(5+t)(1+t)=(5+t)/(1+t)
易錯點
常常有同學在計算中未將結果化簡為最簡分式而因此扣分，因此要特別注意結果分式是否還可以化簡。
例如：計算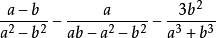
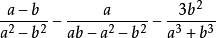
解：原式=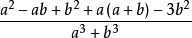
=
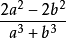
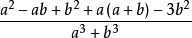
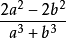
分式運算結果應為最簡分式，上面所得結果的分子、分母有公因式a十b，還應約簡。
所以原式=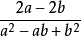
。
