最小正原根問題是一個重要的數論問題。每一個奇素數p都有φ(p-1)個原根，其中最小的那個正整數，稱為最小正原根，記為g(p)。例如，2是模13的最小正原根，記為g(13)=2。若p是各個不同的奇素數，那么模p的最小正原根g(p)的上界是什麼?這就是最小正原根問題。
基本介紹
- 中文名：最小正原根問題
- 外文名：problem on the least positiveprimitive root
- 適用範圍：數理科學
簡介,發展,原根的求法,
簡介
最小正原根問題是一個重要的數論問題。每一個奇素數p都有φ(p-1)個原根，其中最小的那個正整數，稱為最小正原根，記為g(p)。例如，2是模13的最小正原根，記為g(13)=2。若p是各個不同的奇素數，那么模p的最小正原根g(p)的上界是什麼?這就是最小正原根問題。
根據實際計算得出的大量數據，人們猜想，當p充分大時，應有g(p)<kpε，其中ε是一個任意小的正數，而k是與p無關的常數。但是，這個猜測直到現在還沒被證實。
發展
華羅庚於1942年套用狄利克雷特徵函式的概念及三角和的估值方法，在估計最小正原根的上界方面，得到了很好的結果，他證明了：g(p)<2rp1/2，其中r是φ(p)=p-1的不同質因數的個數。
1959年，王元證明了g(p)=O(p1/4+ε)。
原根的求法
若a對模奇素數p的階為d，d<φ(p)，則a1,a2,...,ad不是模p的原根，因此要求p的原根，先列出模p的簡化剩餘系1,2,...,p-1。首先取a=2，求得2對模p的階為d，若d=p-1，則2即為p的原根。若d<p-1，則在1,2,...,p-1中消去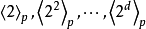
各數。在1,2,...,p-1中剩下的數再取一數，重複以上方法，直到1,2,...,p-1中剩下φ(p-1)個數，因為奇素數p恰有φ(p-1)個原根，因此這φ(p-1)個數都是p的原根。上述求原根的方法稱為消去法。
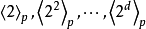
求一個不大的素數為模的原根，目前還沒有一個計算量較小的方法。1927年，阿廷（Artin，E.）猜測：如果一個正整數a非平方數，則存在無窮多個素數p以a為原根。特別地，猜想2，3等都是無限多個素數的原根，這個猜想迄今仍未獲得證明。
