基本介紹
- 中文名:最小數原理
- 外文名:minimum principle
- 所屬學科:數學
- 相關概念:自然數集、實數集、非空子集等
基本介紹,用最小數原理解決存在性問題,最小數原理與反證法相結合,最小數原理與無窮遞降法相結合,
基本介紹
集合理論的重要性在於它的方法論意義,我們知道,有些數學問題所涉及的各個元素的地位是不均衡的,其中的某個極端元素往往具有優於其他元素的特殊性質,能為解題提供方便,而利用這種極端性的依據之一就是有關集合的一條簡單性質。
最小數原理Ⅱ設M是實數集的一個有限的非空子集,則M中必有最小數。
推論 設M是實數集的一個有限的非空子集,則M中必有最大數。
用最小數原理解決存在性問題
由於最小數原理實際上是一個存在性定理,因而與證明大量存在性問題有著密切的關係,運用最小數原理處理存在性問題的關鍵首先是構造滿足某種性質的數集M,然後利用M中的最小數證明命題。
【例1】設S為整數的非空集,滿足:
(1)如果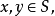 那么
那么
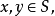

(2)如果 那么
那么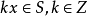 ,
,

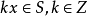
求證:在S中存在一個整數d,使得S由d的所有倍數組成。
證明:若S={0},則命題顯然成立。
若S≠{0},設S+為S中所有正數組成的集合,則S+≠∅(這是因為,S非空,存在非零c∈S,由條件(1)知,0=c-c∈S,-c=0-c∈S,在c,-c中至少有一個為正)。從而S+中有最小數,記為d,由(2),nd∈S(n∈Z),即{nd|n∈Z} S。
S。

另一方面,對任意的h∈S有h=nd+r,0≤r<d,由(1)知,r=h-nd∈S,再由d是屬於S的最小正整數,故只可能r=0,即h=nd.所以S {nd|n∈Z}。
{nd|n∈Z}。

所以S={nd|n∈Z},命題成立。
【例2】若干人聚會,其中某些人彼此認識.已知,如果某兩人在聚會者中有相同數目的熟人,則他倆便沒有共同的熟人。證明:若聚會者中有人至少有20個熟人,則必然也有人恰好有20個熟人。
證明: 我們考慮聚會者中熟人最多的某個人(若這樣的人不止一個,則任取其中一個),記為A,設A共認識n個人,這些人設為 顯然n≥20。
顯然n≥20。

由於 中任意兩人
中任意兩人 與
與 都認識A,即A是他倆的共同熟人,由已知可知
都認識A,即A是他倆的共同熟人,由已知可知 與
與 的熟人數目不等,又
的熟人數目不等,又 的熟人數目均不超過n,且至少有1個熟人,於是他們的熟人數目恰好為1,2,…,n.
的熟人數目均不超過n,且至少有1個熟人,於是他們的熟人數目恰好為1,2,…,n.






由於n≥20,故數20在上述數列中出現,於是 中有人恰好有20個熟人。
中有人恰好有20個熟人。

最小數原理與反證法相結合
【例3】一次10名選手參加的循環賽中無平局,勝者得1分,負者得0分,證明:各選手得分的平方和不超過285。
證明:由於得分的情況僅有有限多種,其中必有一種的平方和取最大值,這時各選手的得分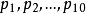 必互不相同,因為若
必互不相同,因為若 ,則改變選手i與j之間的勝負,即用
,則改變選手i與j之間的勝負,即用 來代替
來代替 時,由於
時,由於
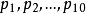




於是,在 時,
時, 最大,這時的值
最大,這時的值 時。
時。



所以各選手得分的平方和不超過285。
【例4】某地區網球俱樂部有20名成員,舉行14場單打比賽,每人至少上場一次。求證:必有6場比賽,其12個參賽者各不相同。
證明: 以無序對 表示參加第 j 場的比賽選手.並記
表示參加第 j 場的比賽選手.並記

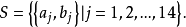
設M為S的一個非空子集,且M中所含選手對中出現的所有選手互不相同,顯然這樣的子集存在有限多個,設這種子集中元素個數最多的一個為 顯然,只需證明r ≥6。
顯然,只需證明r ≥6。

假設 r≤5,由於 是S的選手互異的集合中元素最多的集合,故
是S的選手互異的集合中元素最多的集合,故 中未出現過的20-2r名選手之間互相沒有比賽,否則與
中未出現過的20-2r名選手之間互相沒有比賽,否則與 的定義矛盾,這意味著這20-2r名選手所參加的比賽一定是同
的定義矛盾,這意味著這20-2r名選手所參加的比賽一定是同 中2r名選手進行的,由於已知每名選手至少參加一場比賽,故除了
中2r名選手進行的,由於已知每名選手至少參加一場比賽,故除了 中的 r 場比賽之外,至少還要進行20-2r,一場比賽,即總的比賽場數至少為
中的 r 場比賽之外,至少還要進行20-2r,一場比賽,即總的比賽場數至少為





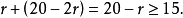

最小數原理與無窮遞降法相結合
所謂無窮遞降法是這樣一種解題模式:在對問題作適當假設的前提下,構造某個無窮遞降過程,但從問題本身看,這個過程應當是有限的,從而產生了矛盾,這說明假設不對,從而肯定了原命題的正確性,有時候我們可以讓這個無窮遞降的過程從某個最小(或最大)的元素出發,這樣就把最小數原理與無窮遞降法聯繫在一起了。
【例5】證明:方程
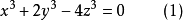

證明: 假設方程(1)有正整數解,設 是方程(1)的所有正整數解中x最小的一組解,由於
是方程(1)的所有正整數解中x最小的一組解,由於


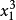














下例的解法與無窮遞降法有某些類似之處.
【例6】在某個星系的每一個星球上,都有一位天文學家在觀測最近的星球,若每兩個星球間的距離都不相等,證明:當星球的個數為奇數時,一定有一個星球任何人都看不到。
證明: 設有n個星球(同時也表示n個天文學家) ,n為奇數,這些星球兩兩之間的距離所成的集合是有限集,故必有最小值,不妨設
,n為奇數,這些星球兩兩之間的距離所成的集合是有限集,故必有最小值,不妨設 最小。
最小。


除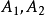 外還有n-2個星球和n-2位天文學家,假若他們當中至少有一位看見已選出的星球,例如A3看見A2,如果誰也看不見A3,則結論成立;否則還有一位天文學家如A4可看見A3,如果誰也看不見A4,結論同樣成立;否則還有一位天文學家如A5可看見A4,仿此下去,由於上述過程中前面星球上的天文學家看不見後面的行星,而n是一個有限數,必然有最後一顆星球任何人都看不到。
外還有n-2個星球和n-2位天文學家,假若他們當中至少有一位看見已選出的星球,例如A3看見A2,如果誰也看不見A3,則結論成立;否則還有一位天文學家如A4可看見A3,如果誰也看不見A4,結論同樣成立;否則還有一位天文學家如A5可看見A4,仿此下去,由於上述過程中前面星球上的天文學家看不見後面的行星,而n是一個有限數,必然有最後一顆星球任何人都看不到。
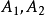
如果其他天文學家都看不到A1,A2,則再從n-2顆星球中選擇距離最近的兩個。依此類推,因為n是奇數,所以最後存在一顆星球,任何人都看不見它。

