Prim

普里姆算法（Prim算法），圖論中的一種算法，可在加權連通圖里搜尋最小生成樹。意即由此算法搜尋到的邊子集所構成的樹中，不但包括了連通圖裡的所有頂點（英語：Vertex (graph theory)），且其所有邊的權值之和亦為最小。該算法於1930年由捷克數學家沃伊捷赫·亞爾尼克（英語：Vojtěch Jarník）發現；並在1957年由美國計算機科學家羅伯特·普里姆（英語：Robert C. Prim）獨立發現；1959年，艾茲格·迪科斯徹再次發現了該算法。因此，在某些場合，普里姆算法又被稱為DJP算法、亞爾尼克算法或普里姆－亞爾尼克算法。

基本介紹

• 中文名：普里姆算法
• 外文名：Prim Algorithm
• 別稱：最小生成樹算法
• 提出者：沃伊捷赫·亞爾尼克（Vojtěch Jarník）
• 提出時間：1930年
• 套用學科：計算機，數據結構，數學（圖論）
• 適用領域範圍：套用圖論知識的實際問題
• 算法：貪心

算法描述

1).輸入：一個加權連通圖，其中頂點集合為V，邊集合為E；

2).初始化：V_new = {x}，其中x為集合V中的任一節點（起始點），E_new = {},為空；

3).重複下列操作，直到V_new = V：

a.在集合E中選取權值最小的邊<u, v>，其中u為集合V_new中的元素，而v不在V_new集合當中，並且v∈V（如果存在有多條滿足前述條件即具有相同權值的邊，則可任意選取其中之一）；

b.將v加入集合V_new中，將<u, v>邊加入集合E_new中；

4).輸出：使用集合V_new和E_new來描述所得到的最小生成樹。

時間複雜度

最小邊、權的數據結構	時間複雜度（總計）
鄰接矩陣、搜尋	O(V^2)
二叉堆（後文偽代碼中使用的數據結構）、鄰接表	O((V + E) log(V)) = O(E log(V))
斐波那契堆、鄰接表	O(E + V log(V))

通過鄰接矩陣圖表示的簡易實現中，找到所有最小權邊共需O（V）的運行時間。使用簡單的二叉堆與鄰接表來表示的話，普里姆算法的運行時間則可縮減為O(ElogV)，其中E為連通圖的邊數，V為頂點數。如果使用較為複雜的斐波那契堆，則可將運行時間進一步縮短為O(E+VlogV)，這在連通圖足夠密集時（當E滿足Ω（VlogV）條件時），可較顯著地提高運行速度。

圖例描述

圖例	說明	不可選	可選	已選（Vnew）
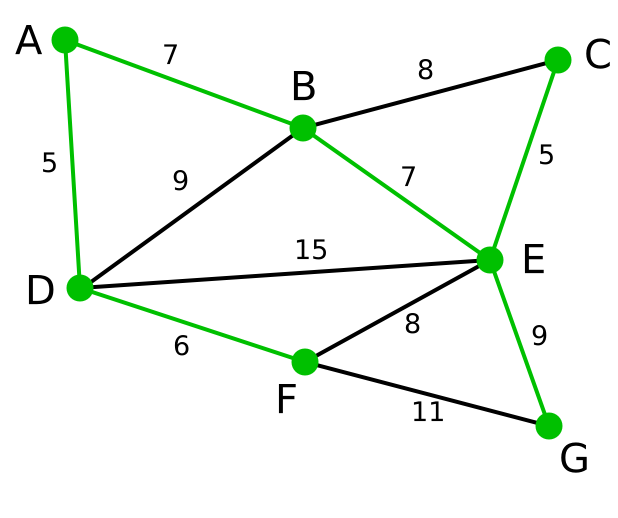
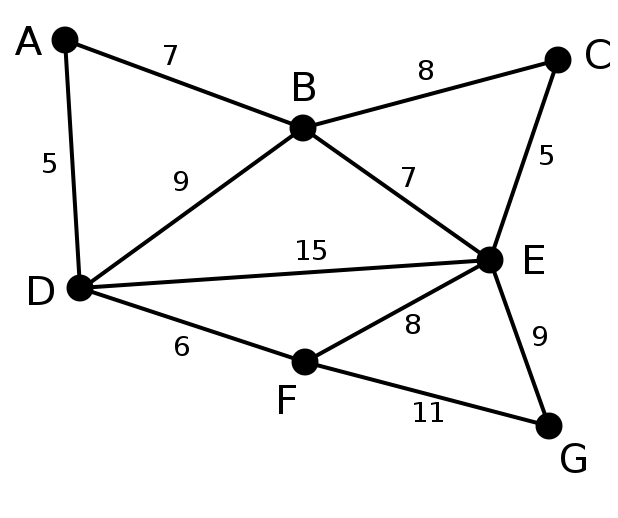	此為原始的加權連通圖。每條邊一側的數字代表其權值。	-	-	-
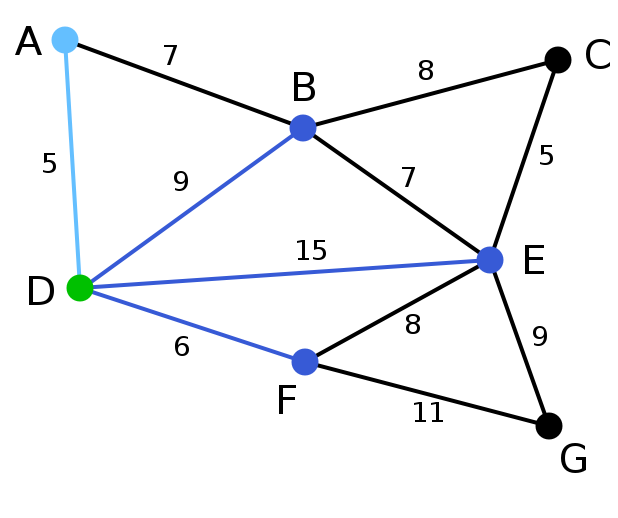	頂點D被任意選為起始點。頂點A、B、E和F通過單條邊與D相連。A是距離D最近的頂點，因此將A及對應邊AD以高亮表示。	C, G	A, B, E, F	D
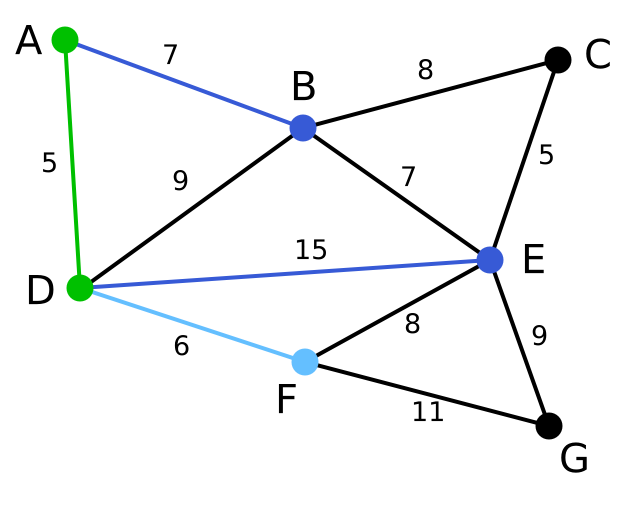	下一個頂點為距離D或A最近的頂點。B距D為9，距A為7，E為15，F為6。因此，F距D或A最近，因此將頂點F與相應邊DF以高亮表示。	C, G	B, E, F	A, D
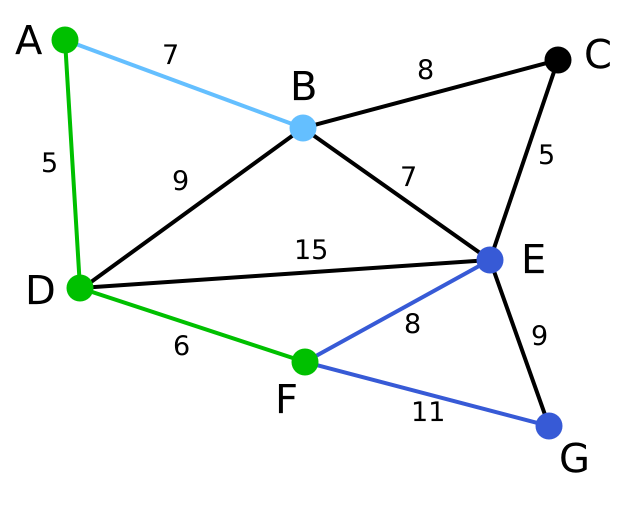	算法繼續重複上面的步驟。距離A為7的頂點B被高亮表示。	C	B, E, G	A, D, F
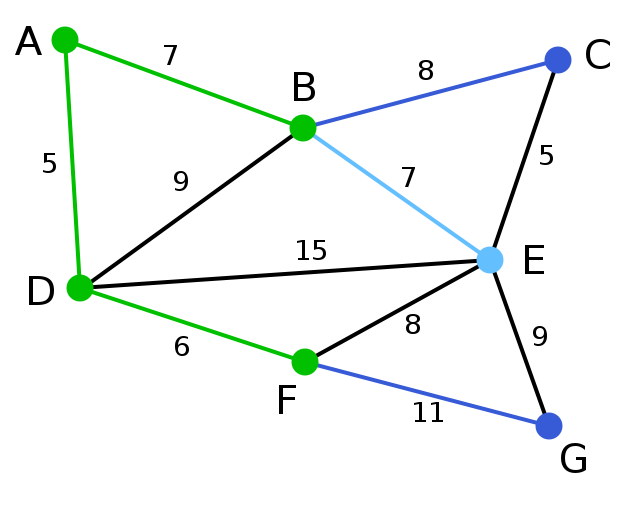	在當前情況下，可以在C、E與G間進行選擇。C距B為8，E距B為7，G距F為11。點E最近，因此將頂點E與相應邊BE高亮表示。	無	C, E, G	A, D, F, B
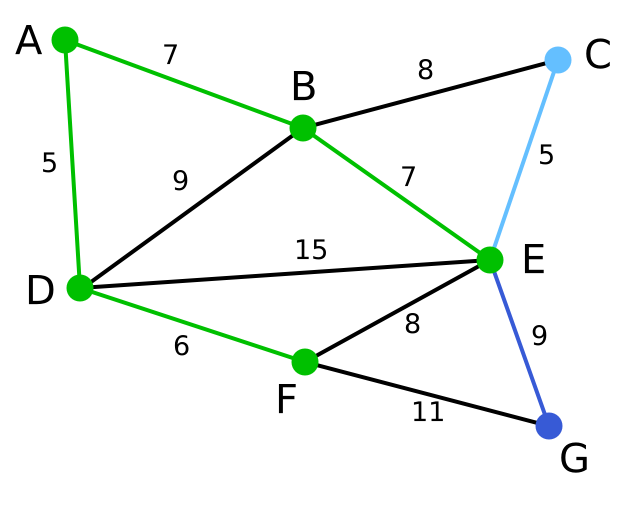	這裡，可供選擇的頂點只有C和G。C距E為5，G距E為9，故選取C，並與邊EC一同高亮表示。	無	C, G	A, D, F, B, E
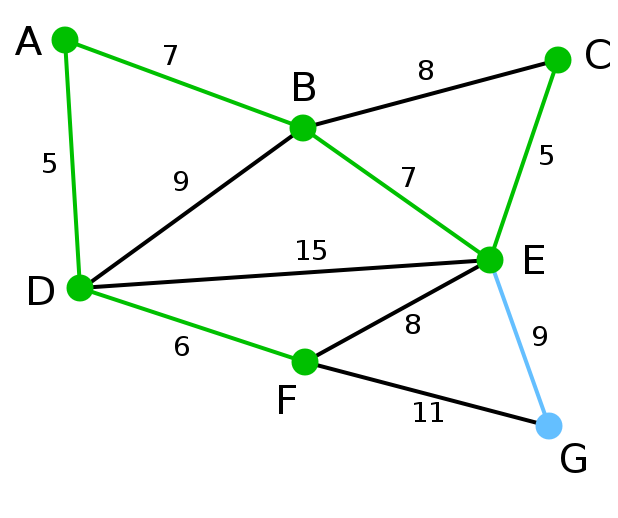	頂點G是唯一剩下的頂點，它距F為11，距E為9，E最近，故高亮表示G及相應邊EG。	無	G	A, D, F, B, E, C
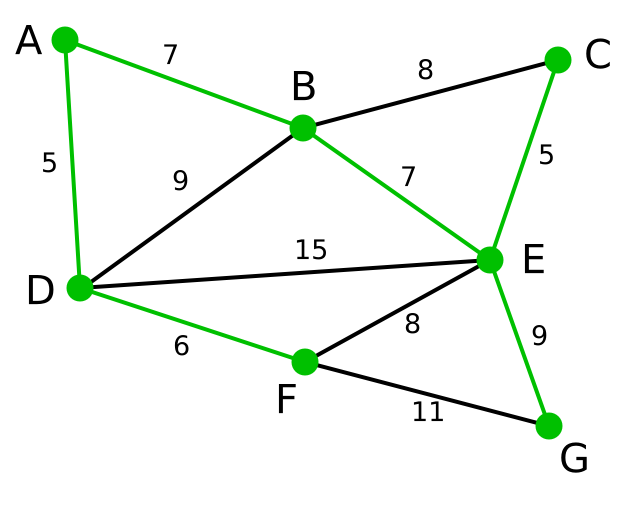	現在，所有頂點均已被選取，圖中綠色部分即為連通圖的最小生成樹。在此例中，最小生成樹的權值之和為39。	無	無	A, D, F, B, E, C, G

代碼

PASCAL代碼

programprim;constmap:array[1..6,1..6]ofinteger=((0,6,1,5,0,0),(6,0,5,0,3,0),(1,5,0,5,6,4),(5,0,5,0,0,2),(0,3,6,0,0,6),(0,0,4,2,6,0));//樣例輸入vari,j,l:integer;min,minn:longint;f,d:array[1..6]ofinteger;s:array[1..6,1..3]ofinteger;v,p:setof1..6;beginl:=1;p:=[];v:=[];fori:=2to6dov:=v+[i];p:=p+[1];fori:=1to6dof[i]:=1000;//還可以寫成filldword(f,sizeof(f)div2,1000)f[1]:=0;fori:=1to6dod[i]:=0;//還可以寫成fillchar(d,sizeof(d),0);s[1,3]:=0;fori:=1to5dobeginmin:=1000;forj:=1to6dobeginif(f[j]>map[l,j])and(jinv)and(map[l,j]<>0)thenbeginf[j]:=map[l,j];d[j]:=l;end;if(f[j]<min)and(f[j]>0)thenbeginmin:=f[j];minn:=j;end;writeln(d[j]);end;f[minn]:=0;v:=v-[minn];p:=p+[minn];s[i,1]:=d[minn];l:=minn;s[i,2]:=minn;s[i,3]:=min;end;fori:=1to5dowrite(s[i,1],'to',s[i,2],'=',s[i,3],'-->');readln;end.

c代碼

#include<stdio.h>#include<stdlib.h>#definemax1000000000;inta[1001][1001],d[1001],p[1001];intmain(){inti,j,k,m,n,min,ans,t;intx,y,z;scanf("%d%d",&n,&m);for(i=1;i<=m;i++){scanf("%d%d%d",&x,&y,&z);a[x][y]=z;a[y][x]=z;}for(i=1;i<=n;i++)d[i]=1000000000;d[1]=0;for(i=2;i<=n;i++){min=max;for(j=1;j<=n;j++)if(!p[j]&&min>d[j])min=d[j];t=j;}p[t]=j;for(j=1;j<=n;j++)if(a[t][j]=0&&d[j]>a[t][j]){d[j]=a[t][j];ans+=min;}printf("%d",ans);return0;}

C++代碼

#defineMAXN1000#defineINF1<<30intclosest[MAXN],lowcost[MAXN],m;//m為節點的個數intG[MAXN][MAXN];//鄰接矩陣intprim(){for(inti=0;i<m;i++){lowcost[i]=INF;}for(inti=0;i<m;i++){closest[i]=0;}closest[0]=-1;//加入第一個點，-1表示該點在集合U中，否則在集合V中intnum=0,ans=0,e=0;//e為最新加入集合的點while(num<m-1)//加入m-1條邊{intmicost=INF,miedge=-1;for(inti=0;i<m;i++)if(closest[i]!=-1){inttemp=G[e][i];if(temp<lowcost[i]){lowcost[i]=temp;closest[i]=e;}if(lowcost[i]<micost)micost=lowcost[miedge=i];}ans+=micost;closest[e=miedge]=-1;num++;}returnans;}

時間複雜度

這裡記頂點數v，邊數e
鄰接矩陣:O(v) 鄰接表:O(elog2v)