斯蒂爾傑斯矩陣(Stieltjes matrix) M矩陣的重要子類,這一矩陣類在塊疊代法收斂性的討論中以及線性互余等問題中有著重要的套用,設AEK為對稱矩陣,則稱A為斯蒂爾傑斯矩陣。
基本介紹
- 中文名:斯蒂爾傑斯矩陣
- 外文名:Stieltjes matrix
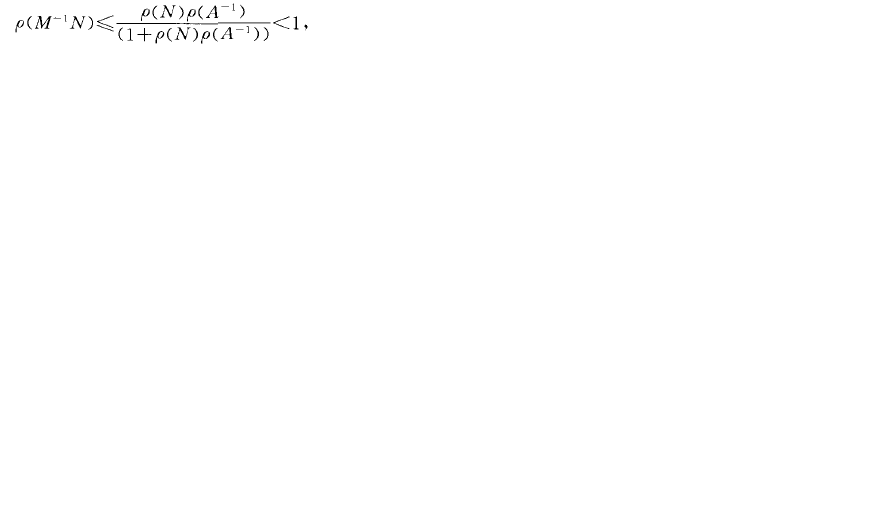
斯蒂爾傑斯矩陣(Stieltjes matrix) M矩陣的重要子類,這一矩陣類在塊疊代法收斂性的討論中以及線性互余等問題中有著重要的套用,設AEK為對稱矩陣,則稱A為斯蒂爾傑斯矩陣。
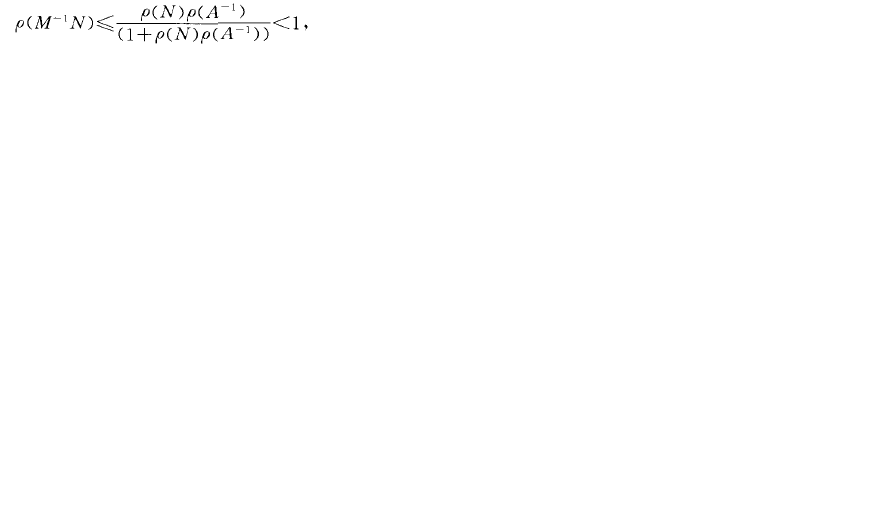
斯蒂爾傑斯矩陣(Stieltjes matrix) M矩陣的重要子類,這一矩陣類在塊疊代法收斂性的討論中以及線性互余等問題中有著重要的套用,設AEK為對稱矩陣,則稱A為斯蒂爾傑斯矩陣。介紹由定義,斯蒂爾傑斯矩陣必為正定...
傅立葉-斯蒂爾傑斯變換(Fourier-Stieltjes transform)是經典傅立葉-斯蒂爾傑斯變換的推廣。簡介 傅立葉-斯蒂爾傑斯變換是經典傅立葉-斯蒂爾傑斯變換的推廣。設G為局部緊交換群,Ĝ為G的對偶群,設M(G)為G上有界的正則複測度全體所成的集。對μ∈M(G),定義Ĝ上的函式 :其中=γ(x)為G上的特徵標,稱 ...
要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。環論 一個環是一個集合R,其中有兩個合成運算,叫作加法和乘法,對有序對a,b,...
5·2 矩陣 5·3 線性方程組 5·4 線性空間 5·5 線性變換 5·6 若爾當標準形 5·7 二次型 5·8 歐幾里得空間 第六章 微積分學 6·1 分析基礎 6·2 微分學 6·3 微分學的套用 6·4 不定積分 6·5 定積分 6·6 重積分 6·7 定積分與重積分的套用 6·8 斯蒂爾傑斯積分 6·9 曲線積分與...
11143黎曼-斯蒂爾傑斯積分 11144泛函分析 11145泛函式 11146譜論 11147線性運算元 11148廣義函式 11149變分法 11150大範圍變分法 11151函式逼近論 11152傅立葉分析 11153三角級數與傅立葉級數 11154傅立葉積分與傅立葉變換 11155凸分析 11156非標準分析 12157微分方程 12158常微分方程 12159抽象空間微分方程 12160泛函微分...
要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。完全環 完全環是一類具有同調性質的環。設R是環,若任意左R模有投射包,則稱R為左...
要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。代數K理論 代數K理論20世紀60年代發展起來的一個代數學分支。它的起源可追溯到1958年...
要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。合環 合環是一類特殊環。對於一個雙模,若它有一個合成列且其中的合成因子都是平衡...
要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。除環 在抽象代數中,除環是一個非零環,其中每個非零元素a都具有乘法逆,即具有x·...
要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。單環 與群論中單群類相對應的基本環類。一個環(代數)R,若只有平凡理想(即除R和...
要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。除環 亦稱體或斜域。接近於域的一類條件很強的環。設R是一個有單位元的環.若R中...
縱觀勒貝格積分和勒貝格-斯蒂爾傑斯積分理論,不難發現它們都有三個基本要素。第一,一個基本空間(即n維歐幾里得空間 R )以及這個空間的某些子集構成的集類即L(勒貝格)可測集或某L-S(勒貝格-斯蒂爾傑斯)可測集全體,這個集類對集的代數運算和極限運算封閉。第二,一個與這個集類有關的函式類(即L可測函式...
n維歐氏空間中有自然的度量ds^2=(dx_1)^2+...+(dx_n)^2。它的矩陣表示就是單位矩陣。歐氏空間中的子流形當然也就自然地誘導出一個度量。曲線和曲面的微分幾何里,我們都是把曲線曲面視為三維空間的子流形,所以自然賦予了度量結構。黎曼空間 愛因斯坦的廣義相對論告訴我們,引力並不是真正的力,而是反映...
要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。微分 微分是微積分的重要概念之一。設函式y=f (x)在點x₀的某個鄰域內有定義。
要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。環論 一個環是一個集合R,其中有兩個合成運算,叫作加法和乘法,對有序對a,b,...
要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。賦值 環A上的賦值是從A到R的區間[0,+∞]中滿足如下條件的映射v:a) 若且唯若...
要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。環論 環論是研究環的性質及其運算規律的代數分支學科。近代環論也包含了非結合代數。
環也是對於交與對稱差運算封閉的集類,並按這兩種運算成為布爾環。要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。
要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。同態 設E與F為兩個群胚,它們的合成法則分別記為⊥與⊤。 稱從E到F中的映射f是...
這樣,莫比烏斯變換可以表述為行列式非零的復矩陣;兩個矩陣產生同樣的莫比烏斯變換若且唯若他們只差一個非零常數。如果賦予黎曼球面富比尼-施圖迪度量,則不是所有的莫比烏斯變換是等度的;例如膨脹和平移就不是。套用 複分析中,複平面(或者任何黎曼曲面)上的的亞純函式是兩個全純函式f和g的比值f / g.作為到...
他的名字出現在黎曼ζ函式、黎曼積分、黎曼引理、黎曼流形、黎曼空間、黎曼映照定理、黎曼-希爾伯特問題、柯西-黎曼方程、黎曼思路迴環矩陣中。著作 黎曼的著作主要有:《單複變函數一般理論的基礎》《關於以幾何學為基礎的假設》《藉助三角級數表示函式的可能性》《數學物理的微分方程》(與韋伯合著)、《橢圓函式論》《...
