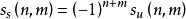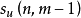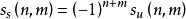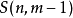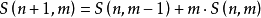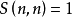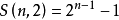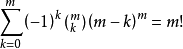斯特林數

在組合數學，Stirling數可指兩類數，第一類Stirling數和第二類Stirling數，都是由18世紀數學家James Stirling提出的。

Stirling數有兩種，第一類和第二類Stirling數，它們自18世紀以來一直吸引許多數學家的興趣，如歐拉、柯西、西爾沃斯特和凱萊等。後來哥本哈根（Copenhagen）大學的尼爾森（Niels Nielsen，1865-1931）提出了"Stirlingschen Zahlen erster Art" [第一類Stirling數]和"Stirlingschen Zahlen zweiter Art" [第二類Stirling數]，首次把這兩類數冠以「Stirling數」之名 。因為蘇格蘭數學家斯特林（J. Stirling, 1692-1770）首次發現這些數並說明了它們的重要性。

基本介紹

• 中文名：斯特林數
• 外文名：Stirling number
• 發現者：James Stirling
• 符號表示：兩類分別是s(n,m)和S(n,m)

歷史

Stirling數的概念由J.Stirling於1730年提出，並在他的著作《Methodous Differentialis》中首次使用。

1958年，Riordan首先套用s(n,k)和S(n,k)來分別表示第一類Stirling數和第二類Stirling數，1770年，L.Lagrenge推導出了第一類Stirling數的遞推關係和數論的性質。而P.S.Lapace和A.Cauchy則在第二類Stirling數的逼近理論上取得了一些成果。1933年，Ch.Jordan在他的一篇論文中對Stirling數做了徹底的闡述，並給出了一些Stirling數的重要性質。

Stirling數概念

Stirling數出現在許多組合枚舉問題中。對第一類Stirling數 ，也可記為 。表示將 n 個不同元素構成m個圓排列的數目。同時還分為無符號第一類Stirling數 和帶符號第一類Stirling數 。

第二類Stirling數 ，同時可記為 [與第一類的表示有大小寫的區別]。其表示將n個不同的元素分成m個集合的方案數。

第一類Stirling數

定義

第一類Stirling數表示將 n 個不同元素構成m個圓排列的數目。又根據正負性分為無符號第一類Stirling數 和帶符號第一類Stirling數 。有無符號Stirling數分別表現為其升階函式和降階函式的各項係數[類似於二項式係數]，形式如下：

對於有無符號Stirling數之間的關係有 。組合數學中的第一類Stirling數一般指無符號的第一類Stirling數。意思是n個不同元素構成m個圓排列的方案數。

遞推式

無符號第一類Stirling數的遞推式可以從其定義來推導：

考慮其定義如果要將n+1元素構成m個圓排列，考慮第n+1個元素：

（1）如果n個元素構成了m-1個圓排列，那么第n+1個元素獨自構成一個圓排列。方案數：

（2）如果n個元素構成了m個圓排列，將第n+1個元素插入到任意元素的左邊。方案數：

綜合兩種情況得：

而有符號的第一類Stirling數可以從其表示的降階函式歸納證明（簡單寫如下）：

依次把 在左右兩邊的係數提取出來得：

“pascal”三角形

二項式係數 可以構成一個楊輝三角（pascal三角形）。同樣第一類Stirling數同樣也可以構成一個三角，可以由此分析其性質。

	無符號Stirling數	有符號Stirling數
n=0	1	1
n=1	0 1	0 1
n=2	0 1 1	0 -1 1
n=3	0 2 3 1	0 2 -3 1
n=4	0 6 11 6 1	0 -6 11 -6 1
n=5	0 24 50 35 10 1	0 24 -50 35 -10 1
n=6	0 120 274 225 85 15 1	0 -120 274 -225 85 -15 1
n=7	0 720 1764 1624 735 175 21 1	0 720 -1764 1624 -735 175 -21 1

性質

無符號Stirling數有如下性質：

①

②

③

④

⑤

⑥

⑦

⑧ 證明可令升階函式中的x=1，比較兩邊係數。

有符號stirling性質類似：

①

⑧ ，注意 。證明可令降階函式中的x=1，比較兩邊係數。

套用舉例

第一類Stirling除了表示可以表示升階函式和降階函式的係數之外還可以套用到一些實際問題上。例如很經典的解鎖倉庫問題。

問題說明如下：有n個倉庫，每個倉庫有兩把鑰匙，共2n把鑰匙。同時又有n位官員。問如何放置鑰匙使得所有官員都能夠打開所有倉庫？（只考慮鑰匙怎么放到倉庫中，而不考慮官員拿哪把鑰匙。）那如果官員分成m個不同的部，部中的官員數量和管理的倉庫數量一致。那么有多少方案使得，同部的所有官員可以打開所有本部管理的倉庫，而無法打開其他部管理的倉庫？（同樣只考慮鑰匙的放置。）

第一問很經典，就是打開將鑰匙放入倉庫構成一個環：1號倉庫放2號鑰匙，2號倉庫放3號鑰匙……n號倉庫放1號鑰匙。這種情況相當於鑰匙和倉庫編號構成一個圓排列方案數是 種。

而第二問就對應的將n個元素分成m個圓排列，方案數就是第一類無符號Stirling數 。如要要考慮官員的情況，只需再乘上 即可。

母函式

固定m將n看作是項數，母函式表示如下：

該式子的通項公式求解略微繁瑣，這邊僅給出其生成函式。更具體的參考維基中的通項定義。

第二類Stirling數

定義

第二類Stirling數實際上是集合的一個拆分，表示將n個不同的元素拆分成m個集合的方案數，記為 或者 。和第一類Stirling數不同的是，集合內是不考慮次序的，而圓排列是有序的。常常用於解決組合數學中幾類放球模型。描述為：將n個不同的球放入m個無差別的盒子中，要求盒子非空，有幾種方案？

第二類Stirling數要求盒子是無區別的，所以可以得到其方案數公式：

遞推式

第二類Stirling數的推導和第一類Stirling數類似，可以從定義出發考慮第n+1個元素的情況，假設要把n+1個元素分成m個集合則分析如下：

（1）如果n個元素構成了m-1個集合，那么第n+1個元素單獨構成一個集合。方案數 。

（2）如果n個元素已經構成了m個集合，將第n+1個元素插入到任意一個集合。方案數 m*S(n,m) 。

綜合兩種情況得：

“pascal”三角形

n=0	1
n=1	0 1
n=2	0 1 1
n=3	0 1 3 1
n=4	0 1 7 6 1
n=5	0 1 15 25 10 1
n=6	0 1 31 90 65 15 1
n=7	0 1 63 301 350 140 21 1
n=8	0 1 127 966 1701 1050 266 28 1
n=9	0 1 255 3025 7770 6951 2646 462 36 1

性質

①

②

③

④

⑤

⑥

⑦

⑧

⑨ ， 是貝爾數。

推論

（1） 若n<m

（2）因為S(m,m)=1，所以有

套用舉例

第二類Stirling數主要是用於解決組合數學中的幾類放球模型。主要是針對於球之前有區別的放球模型：

（1）n個不同的球，放入m個無區別的盒子，不允許盒子為空。

方案數： 。這個跟第二類Stirling數的定義一致。

（2）n個不同的球，放入m個有區別的盒子，不允許盒子為空。

方案數： 。因盒子有區別，乘上盒子的排列即可。

（3）n個不同的球，放入m個無區別的盒子，允許盒子為空。

方案數： 。枚舉非空盒的數目便可。

（4）n個不同的球，放入m個有區別的盒子，允許盒子為空。

①方案數： 。同樣可以枚舉非空盒的數目，注意到盒子有區別，乘上一個排列係數。

②既然允許盒子為空，且盒子間有區別，那么對於每個球有m中選擇，每個球相互獨立。有方案數： 。

上述式子可以套用於第二類Stirling數通項的求解。

通項公式：

這個通項公式有多種方法推導。常用的有容斥原理，母函式和等式求解等。

一、容斥原理。

容斥原理最為通俗易懂。

①為了區分集合，給集合上個標號順序，最後答案再除 即可。

②既然盒子有區別，那么先不考慮空盒，對於每個元素有m種選擇，方法數是： 。顯然包含了空盒的情況，且空盒數量是大於等於0的。為了方便說明，這邊設存在空盒數是h的情況是 種。那么便有 ，以及 。

③自然想到計算空盒數大於等於1的情況就能求解。那么先選定一個空盒，剩餘的再隨便放置，方案數是： 。那么有h的空盒的情況被計算了幾次？因為空盒必須要有一個出現在被選定的位置，那么重複數量是： 。

④對於更一般情況，計算空盒數不小於k的情況有 ，而產生h空盒的重複次數是 。那么就有 。

⑤要消除掉這種組合數為係數的項要利用到容斥原理。 。那么就有：

交換一些累加符號順序得：

右邊=

解得：

二、母函式

母函式解法最為簡便。

首先，還是一樣先區分集合。因母函式一般是一維的項數，這邊固定集合數量為m，設n為項數。則有：

對於每個集合因為元素之間不同，且集合非空，生成函式（母函式）為： 。

因為有m個集合，且互不相同，利用乘法法則和二項式展開有：

對上式中的 使用泰勒張開（指數型母函式）：

提取出上述等式兩邊 的係數有：

同樣可以求得：

三、利用等式求解

這是套用舉例中的一個等式：

顯然看到，要消除係數，嘗試不同的m值有：

發現排列數發生變化，為了抵消其變化等式兩邊同時乘上 得：

要消去組合數係數 利用一正一負累加：

交換求和順序有：

右邊

同樣可以求得通項公式：

兩類Stirling數之間的關係

兩類Stirling數之間的遞推式和實際含義很類似，事實上他們之間存在一個互為轉置的轉化關係：

類似於矩陣的對稱轉置關係。