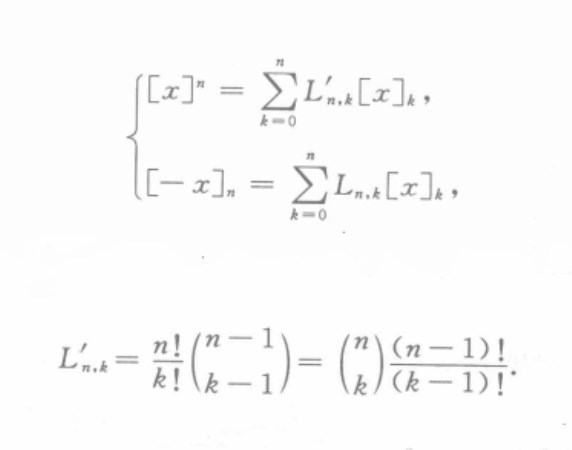拉氏數

拉氏數(Lah number)是一類組合數，它與Stirling數（斯特林數）有密切的關係。分為帶符號的拉氏數和不帶符號的拉氏數，Lah數表示多項式函式空間R[x]中兩組基{[x]_n}與{[x]ⁿ}之間的關係。

基本介紹

• 中文名：拉氏數
• 外文名：Lah number
• 所屬學科：數學（組合學）
• 簡介：一類組合數

基本介紹

拉氏數是一類組合數。

①由恆等式：

(x)_n= L(n，k)[x]_k

或

(x)_n= L(n，k)(-x)_k

定義的拉氏數L(n，k)稱為帶符號的拉氏數

②由恆等式：

(x)ⁿ= L′(n，k)(x)_k

定義的拉氏數L′(n，k)稱為不帶符號的拉氏數：

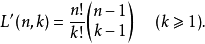
③帶符號、不帶符號的兩種拉氏數L(n，k)和L′(n，n)統稱拉氏數或Lah數。

相關性質

設

則係數L_n,k稱為Lah數，它與Stirling數（斯特林數）有密切的關係。它有以下表達式：

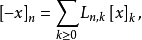
性質1

(1)

(2)

(3)

其中s(n，j)為第一類斯特林數(Stirling)數，S(j，k)為第二類Stirling數。

遞推公式

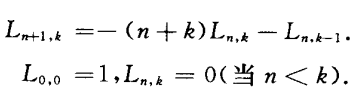
由此可得L_0，1=0(n>0)，L_n，n=(-1)ⁿ。

定義 函式

稱為Lah數的生成函式。

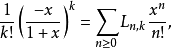
表1為Lah數表（列數為n，行數為k）。

表1 Lah數Ln，k

	0	1	2	3	4	5	6
0	1
1	0	-1
2	0	2	1
3	0	- 6	-6	-1
4	0	24	36	12	1
5	0	-120	- 240	-120	-20	-1
6	0	720	1800	1200	300	30	1