冰雹猜想

冰雹猜想是指：一個正整數x，如果是奇數就乘以3再加1，如果是偶數就析出偶數因數2，這樣經過若干個次數，最終回到1。

無論這個過程中的數值如何龐大，就像瀑布一樣迅速墜落。而其他的數字即使不是如此，在經過若干次的變換之後也必然會到純偶數：16-8-4-2-1的循環。據日本和美國的數學家攻關研究，在小於7*10^11的所有的正整數，都符合這個規律。

基本介紹

• 中文名：冰雹猜想
• 外文名：Collatz Conjecture 
• 別名：3n+1猜想 
• 表達式：Xs+1=(3Xs+1)/2
• 提出者：Lothar Collatz 
• 提出時間：1937年
• 適用領域：算術代數幾何、微分幾何
• 套用學科：抽象代數
• 系朗蘭茲綱領：通過伽羅瓦表示定義自守形式 
• 系分形幾何：以自同構演繹高維空間的三維切叢 

冰雹猜想

冰雹猜想來歷

1976年的一天，《華盛頓郵報》於頭版頭條報導了一條數學新聞。文中記敘了這樣一個故事：

全體自然數被螺旋式吸入黑洞(4,2,1,4)，再以射線(4,2,1,4)射出

70年代中期，美國各所名牌大學校園內，人們都像發瘋一般，夜以繼日，廢寢忘食地玩弄一種數學遊戲。這個遊戲十分簡單：任意寫出一個正整數N，並且按照以下的規律進行變換：

如果是個奇數，則下一步變成3N+1。

如果是個偶數，則下一步變成N/2。

不單單是學生，甚至連教師、研究員、教授與學究都紛紛加入。為什麼這種遊戲的魅力經久不衰？因為人們發現，無論N是怎樣一個數字，最終都無法逃脫回到谷底1。準確地說，是無法逃出落入底部的4-2-1循環，永遠也逃不出這樣的宿命。

這就是著名的“冰雹猜想”。

黑洞4-2-1，視界8，主旋臂3*5+1=32/2=16，奇點(4-1)/3=(2+1)/3=1

強悍的27

冰雹的最大魅力在於不可預知性。英國劍橋大學教授John Conway找到了一個自然數27。雖然27是一個貌不驚人的自然數，但是如果按照上述方法進行運算，則它的上浮下沉異常劇烈：首先，27要經過77步驟的變換到達頂峰值9232，然後又經過34步驟到達谷底值1。全部的變換過程（稱作“雹程”）需要111步，其頂峰值9232，達到了原有數字27的342倍多，如果以瀑布般的直線下落（2的N次方）來比較，則具有同樣雹程的數字N要達到2的111次方。其對比何其驚人！

27的歸一步數要經過多次劇烈波動的奇偶變換，其路徑呈不光滑鋸齒

但是在1到100的範圍內，像27這樣的劇烈波動是沒有的（54等27的2的次方倍數的數除外。

驗證規律

經過遊戲的驗證規律，人們發現僅僅在兼具4k和3m+1（k,m為自然數）處的數字才能產生冰雹猜想中“樹”的分叉。所以在冰雹樹中，16處是第一處分叉，然後是64……以後每隔一節，產生出一支新的支流。

與27形成鮮明對比，2^16是零波動的光滑反比例曲線，呈單調遞減

自從Conway發現了神奇的27之後，有專家指出，27這個數字必定只能由54變來，54又必然從108變來，所以，27之上，肯定可以出現不亞於2n的強大支流——33*2n(n=1，2，3……)，然而，27到4-2-1數列和本流2到4-2-1數列要遙遠的多。按照機械唯物論的觀點，從27開始逆流而上的數列群才能叫做本源，儘管如此，按照“直線下瀉”的觀點，一般依然把1-2-4-8……2n的這一支看作是“幹流”。

又稱角谷猜想，因為是一個名叫角谷的日本人把它傳到中國。

數列驗證法，此方法是根據冰雹猜想的驗證規則而建立的一種驗證方法，是以無限的數列來對付無限的自然數。首項偶數，公差是偶數，那么數列上的所有自然數都是偶數，全體數列除於2，如果首項是奇數公差是偶數，那么數列上全體自然數都是奇數，全體乘上3再加1。如果公差是奇數，首項也是奇數，那么第奇數項必定都是奇數則乘上3再加1，第偶數項必定都是偶數,則除於2。如果公差是奇數，首項是偶數，那么第奇數項必定都是偶數，則除於2，第偶數項必定都是奇數，則乘上3再加1。按照這樣的計算規則計算下去，會遇到許多新的問題，考驗驗證者的智商。比如偶數的通項公式是2n，因為都是偶數所以除於2，得到n，這就是自然數。

按照忽略偶數不記錄的驗證方法進行驗證，第一個被驗證的奇數有可能是能被3整除的奇數，也有可能是不能被3整除的奇數。但是，3x+1以後，所到達所歸結的第二個奇數，以及第三個奇數（假設存在）............整個過程所到達所遇到所歸結所訪問到的每一個奇數，必定都不能再被3整除了。如果都從從能被3整除的奇數開始驗證，路徑上所遇到所歸結的所到達所訪問到的每一個奇數都必定不能再被3整除了，最終都能歸結於1，那么必定遍歷所有的奇數（遍歷是離散數學的概念）。如果都從不能被3整除的奇數開始驗證，那么路徑上所遇到所到達所歸結的所訪問到的每一個奇數必定都不可能再被3整除了，最終都歸結於1（等於說是漏下能被3整除的奇數沒有被驗證）。所以在順向的冰雹猜想驗證過程中，可以把能被3整除的奇數都命名為最起始點的奇數，1是終止點的奇數，而在逆向的冰雹猜想驗證過程中則是相反的，1是最起始點的奇數，而能被3整除的奇數則是終止點的奇數。事實上在驗證的過程中，不能被3整除的奇數，都在存在數量無窮多的上一步的奇數，占1/3的比例是能被3整除的奇數，占2/3的比例是不能被3整除的奇數，這一現象都跟自然數的情況出奇地巧合了.這一規律，無論是單個奇數的驗證方法，還是等差數列驗證法必須遵守。在能被3整除的奇數之前的，只有能被3整除的偶數，沒有任何奇數。

這種新的驗證方法存在缺陷，就是運算不連續，雖然也可以用於驗證爬升或者下降...爬升的時候需要對2進行因式分解......下降的時候需要先把3^n給計算出來....所以比較麻煩.....優點只有一個，那就是當驗證到近乎無限爬升的時候....比如說(2 n-1)*2^（一億）-1的驗證過程就是把一億個2換成一億個3，(2 n-1)*3^（一億）-1，一次性替換，我們需要把3^（一億） 給計算出來，如果按照傳統的驗證方法，你需要把(2 n-1)*2^（一億）-1給算出來，然後再爬升(一億-1)步以後才能得到這個結果......

把奇數分成2類 ：

能被3整除的奇數 通項公式是6(n-1)+3 這一類的奇數是不可以通過3x+1得到的 又叫最起始點的奇數 這一類的奇數不可能發生 病態歸結的，因為從這一類奇數開始計算可以得到其他奇數，而從其他奇數開始計算絕對不能得到這一類的奇數。

再看看7x+1 ,15x+1 ,7x-3 ,15x-7,他們的最起始點的奇數就不只是能被7整除那么簡單了..........

不能被3整除的奇數 通項公式分別是：6（n-1）+1 和6(n-1)+5...他們都是可以通過3x+1得到的，又叫路徑上的奇數或者是過程奇數，有可能，發生主病態歸結點的奇數就在這2類之間。

存在X1，使得X1*3+1之後只能被1個2整除，之後就是奇數，這一類奇數占奇數總量的1/2；

存在X2，使得X2*3+1之後只能被2個2整除，之後就是奇數，這一類奇數占奇數總量的1/4；

存在X3，使得X3*3+1之後只能被3個2整除，之後就是奇數，這一類奇數占奇數總量的1/8；

............................................

我還在許多猜想的擴題中找到許多相類似的規律，只要是存在逆推定理的猜想擴題就存在本規律

只是連除的規律比較混亂........無法總結出總通項公式

以此類推............從逆推定理四出發，可以很方便地找到，X1,X2,X3,X4,X5,X6.........的通項公式

那些方程組的歸結數列不是6（n-1）+1就是6(n-1)+5，只要把被除數帶分別乘與公式-1以後再除3就出來了，

x1=（2*（6(n-1)+5）-1）/3=3+4（n-1）,但是新的問題馬上來了 ，存在N組等差數列能進行N步的奇數運算，每一步都能整除於同一個純偶數，而且之後都是奇數，..........這就叫連除，連除2和4的我都計算出來了，但是連除8 16 32 64 ..........的還沒有算出通項公式，其實這類運算往往都是以3來替換相應的純偶數，首項是拆解意義上的替換，公差則是因式分解意義上的替換.......造成計算困難的原因是：存在數量正無窮多的純偶數，算不完的.

205+8^3*2(n-1) 在驗證過程中就是以3換8,它可以進行至少3次的替換

比如205=128+64+8+5 ....

為了證明冰雹猜想中是否存在無限爬升的現象，我偶然中發現了這一規律。該規律可以作為直接歸結定理的一個推論。

其實，要想研究冰雹猜想的反例的特徵是可以從角谷猜想的深度擴展的擴題中找到的，比如3X-1的猜想中的奇數5和7，就是互相歸結的另外一種死循環的歸結，從5到7，從7到5，從5到7..............沒完沒了，無法得到1，就算驗證1萬年也是如此。我已經證明了，像這種2個自然數之間的病態的互相歸結 在3X-1的猜想中 盡此一個，2個數字，但是這僅僅是主病態歸結，因為5和7都不能被3整除，所以存在數量正無窮大的奇數，和相應的偶數，都被它們牽連了，這些自然數都是無法最終歸結於1的。究竟那些自然數是被牽連的，那些自然數是不被牽連的，這隻有相對應的逆推定理所能做到的了。角谷猜想的原題即使存在反例也是非常巨大的自然數........在來點難度大的，為了證明是否存在這種類似的2個自然數之間互相歸結的情況，我首先假設存在2個數字A和B，從A開始算得到B，從B開始算得到A ,根據角谷猜想的規則建立2個2元1次方程組，解得A和B ，得到2組整數組，分別是A=B=1 A=-5 B=-7 其餘的解都是分數，這就證明了 角谷猜想的原題 在這個問題上沒有反例........絕對不存在2個自然之間的互相歸結 而無法得到1.主病態歸結點的奇數在數量上是有限是，但是牽連的病態歸結點奇數 偶數在數量上都是無限的 雖然只有5和7這2個路徑奇數發生了主病態歸結，無法得到1的自然數在3x-1的猜想中至少占有自然數總量的1/2多一點點的

像這樣的反例，在數量正無窮大的角谷猜想深度擴展題目中有無數多串....有的方程組只能算到一串反例，有的能算到很多串反例........

原題的方程組，至少需要計算 一萬個未知數以上的方程組才能知道反例是否存在 一萬個未知數以下的方程組已經被我證明了 是絕對不存在反例的

分母式是：2^m-3^（n+1）>1 m>n 只需要考慮 2^m>3^（n+1）的一瞬間 即可

當分母式=4^(m+1)-3^(m+1)的時候是平衡點，都是能整除的，但是不是反例，這個時候方程組的解等於1，..........

如果差值之中有1的話 那么就證明 反例存在 而且可以 找出反例子是多少

有多少個1 就存在多少竄反例

就算沒有1 同樣存在可能性會出現反例的。比如5x+1的方程組的分母值取3的時候就存在一串3個非最起始點的奇數的解是13——33——83——13——33，.....只要是掉進原來的數就是該類型的反例，一直反覆不斷，一直到永遠......

化簡版本也就是x+1猜想是不存在任何反例的，原題在一萬個未知數以內的方程組都是絕對不存在反例的，而一萬個未知數以上的方程組，人類的大腦是無法計算的，除非依靠電腦來算。

根據普通的奇數與偶數的描述公式法，即偶數是2n，奇數是2n-1的描述辦法並不符合冰雹猜想的運算。符合冰雹猜想的偶數歸結於奇數的逆向描述公式是：偶數=f(m,n)=(2n-1)*2^m，這是描述偶數歸結於奇數的另外一個公式。同樣是一個2維的平面的數列。由2條互相垂直的射線組成的射面狀的無窮數列。

我最近致力於反例子的研究，有許多成果，無非3大類，對於3X+1的猜想，或者是對於眾多的擴展題目，是否存在無限增大的現象，有存在的理由 ，也有不存在的理由 ，一時之間難下定論......難度都很大的....這些研究成果有助於該猜想的規律化，更規律化，.....導致奇數在驗證過程中爬升的規律已經總結出來了就是以3換2....

函式f(n)通過奇偶疊代織成蜘蛛網，射線為3n+1,螺旋線為(3n+1)/2

一，3x+1猜想的公式

將問題公式化，是解決猜想的必由之路。這是一個疊代公式，有輸入，輸出，反饋，....。

f(n)解析延拓至複平面生成無限嵌套的自相似分形：時空對稱性

.........(1)

這裡公式中每一個X 都是奇數，m=1,2,3，....。直到把3x+1中的偶數析出抵消，使得（1）式右邊是奇數為止。

如果不是1而是其他奇數，就繼續疊代。一直到1為止。

.........(2)

二，範例

例如，代入公式：結束。

例如，,代入公式：；結束。

角谷是說，輸入x =1,3,5,7,9,11，....任何一個奇數，直至無窮，經過（1）疊代，都是（2）式等於1。

需要證明兩個結論以後才有可能完成：

1，任何一個進入疊代以後不會回到，就是不會發生循環。如果發生循環，表明是一個反例，否定了角谷猜想。

2，進入疊代以後數值不會發散，就是不會越來越大直至無窮，而是在一個有限的範圍內更替。

三，倒行逆施

把（2）式中的.......（3）

使得（3）式的有：

=5，21， 85， 341，1365， 5461， 21845， .....。因為這個是把（3）式反推的結果。

例如：

=5，；,

=21，；

=85，；；

這些都是等於1。

.......。

.....（4）

在（4）式二步到位=1的有：3, 13, 53, 113, 227, 909，.....。

......（5）

（5）式這個是把（4）式反推的結果。

例如：

=13，代入公式（3）需要兩步：。

用（5）式即。

用（4）式也可以：。

在（6）式三步使得的有如下形狀：

簡化（7）式:。

形的數：11，17， 75，301，1205，...。因為這個是把（6）式反推的結果。例如

=75需要3步，

；

用（7）式：

用（6）式：

四，3x+1猜想為什麼會成立？

因為（6）式代入（7）式的（8）式，正好分子與分母抵消

....................(8)

五，這是一個二階邏輯問題

只需順著方向證明即可。把n擴展到任意數

..........（9）。

（9）式是說對於任何一個n，總有一個數使得分子與分母相等。

把（7）式擴展的任意一個n：

.........(10)

把（10）式代入（9）式，則分子分母剛剛可以抵消。

（10）式是一個倒裝公式，初始值內部（）包含了未來值部分(),，好比爺爺（初始值）的基因包含了子孫（未來值）的基因，屬於時光倒錯。

屬於無法證明的問題。

本章節文章摘自美國中文網王曉明部落格，點擊：wxmwrk即可查詢。也可查詢中國科學院智慧火花數學欄目。

二，3x+3猜想

什麼是3x+3猜想

3X+3猜想，就是說無論X是什麼整數，如果是奇數就乘以3再加3，如果是偶數就除以，直到最後都是3。

......（1），

其中是指把全部偶數析出。

最後結果一定是：.......。（2）

範例

例如:

=7，7×3 +3=24, 24÷8=3。

=9，9×3+3=30，30÷2=15，15×3+3=48，48÷16=3（回到X=5的狀態）。

=11，11×3+3=36，析出4得9，9→15→3，回到X=5的狀態。

=13，13×3+3=42，21→33→51→39→15→3.(回到X=5狀態）。

=15，回到x=5狀態。

=17，27→21→33→51→39→15→3。回到X=13狀態。

=19，19×3+3=60，回到X=15狀態。

=21，回到X=13狀態。

=23，23×3+3=72,回到X=9狀態。

其中，=53用了43次疊代回到3：

53——81——123——93——141——213——321——483——363——273——411——309——465——699——525——789——1185——1779——1335——501——753——1131——849——1275——957——1437——2157——3237——4857——7287——2733——4101——6153——9231——1731——1299——975——183——69——105——159——15——3.。

=61用了40次疊代回到3：

61——93——141——213——321——483——363——273——411——309——465——699——525——789——1185——1779——1335——501——753——1131——849——1275——957——1437——2157——3237——4857——7287——2733——4101——6153——9231——1731——1299——975——183——69——105——159——15——3.

屬於二階邏輯問題

同3x+1猜想一樣，代入公式以後，分子分母可以抵消，剩下一個分子3。它跟3x+1猜想本質上是一樣的，無法證明。

克拉茨問題

角谷猜想又叫敘古拉猜想。它的一個推廣是克拉茨問題，下面簡要說說這個問題：

50年代開始,在國際數學界廣泛流行著這樣一個奇怪有趣的數學問題:任意給定一個正整數x,如果是偶數,則變換成x/2,如果是奇數,則變換成3x+1.此後,再對得數繼續進行上述變換.例如x=52,可以陸續得出26,13,40,20,10,5,16,8,4,2,1.如果再做下去就得到循環:

(4,2,1).再試其他的正整數也會得出相同的結果.這個叫做敘古拉猜想.

上述變換,實際上是進行下列函式的疊代

{ x/2 (x是偶數)

C(x)=

3x+1 (x是奇數)

問題是,從任意一個正整數開始,經過有限次函式C疊代,能否最終得到循環(4,2,1),或者等價地說,最終得到1?據說克拉茨(L.Collatz)在1950年召開的一次國際數學家大會上談起過,因而許多人稱之為克拉茨問題.但是後來也有許多人獨立地發現過同一個問題,所以,從此以後也許為了避免引起問題的歸屬爭議,許多文獻稱之為3x+1問題.

懸賞征解

克拉茨問題吸引人之處在於C疊代過程中一旦出現2的冪,問題就解決了,而2的冪有無窮多個,人們認為只要疊代過程持續足夠長,必定會碰到一個2的冪使問題以肯定形式得到解決.正是這種信念使得問題每到一處,便在那裡掀起一股"3x+1問題"狂熱,不論是大學還是研究機構都不同程度地捲入這一問題.許多數學家開始懸賞征解,有的500美元,有的1000英鎊.

數學難題

1972年，普林斯頓大學高等研究院教授JH Conway證明Collatz問題的自然概括是算法不可判定的.1990年，哈佛大學數學研究所教授Kurtz和史丹福大學高級研究中心教授Simon 證明，上述問題事實上在算術等級中是不可判定的.日本東京大學的米田信夫已經對240大約是11000億以下的自然數做了檢驗.1992年李文斯(G.T.Leavens)和弗穆蘭(M.Vermeulen)已經對5.6*1013的自然數進行了驗證,均未發現反例.2011年，加州大學著名華人數學天才陶哲軒在其研究部落格WordPress上寫下了這么一段話：“不用說，我沒有解決問題，但我更好地理解為什麼這個猜想是（a）合理的，（b）不太可能被當前的技術證明，我想我會分享我發現的在這個部落格上.”題意如此清晰,明了,簡單,連小學生都能看懂的問題,卻難到了20世紀許多大數學家.著名學者蓋伊(R.K.Guy)在介紹這一世界難題的時候,竟然冠以"不要試圖去解決這些問題"為標題.經過幾十年的探索與研究,人們似乎接受了大數學家厄特希(P.Erdos)的說法:"數學還沒有成熟到足以解決這樣的問題!"有人提議將3x+1問題作為下一個費爾馬問題.

命題證明

引理一:若n=2m,則fm(n)=1 (m∈N)

證明:當m=1時,f(n)=f(2)=2/2=1,命題成立,設當m=k時成立,則當m=k+1時,fk+1(n)=f(fk(2k+1))=

=f(2)=2/2=1.證畢.

引理二:若n=1+4+42+43+...+4k=(4k+1-1)/(4-1) (k∈N),則有f(n)=3n+1=4k+1=22k+2,從而f2k+3(n)=1.

證明:證明是顯然的,省略.

引理三:若n=2m(4k+1-1)/(4-1) (m∈N), 則有fm+2k+3(n)=1.

證明:省略.

定理一

:集合 O={X|X=2k-1,k∈N} 對於變換f(X)是封閉的.

證明:對於任意自然數n,若n=2m,則fm(n)=1,對於n=2k,經過若干次偶變換,必然要變成奇數,所以我們以下之考慮奇數的情形,即集合O的情形.對於奇數,首先要進行奇變換,伴隨而來的必然是偶變換,所以對於奇數,肯定要進行一次全變換.為了直觀起見,我們將奇數列及其全變換排列如下:

k 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51

0 2k-1 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 81 83 85 87 89 91 93 95 97 99 101

1 3k-1 2 5 8 11 14 17 20 23 26 29 32 35 38 41 44 47 50 53 56 59 62 65 68 71 74 77 80 83 86 89 92 95 98 101 104 107 110 113 116 119 122 125 128 131 134 137 140 143 146 149 152

2 3k-2 1 　 4 　 7 　 10 　 13 　 16 　 19 　 22 　 25 　 28 　 31 　 34 　 37 　 40 　 43 　 46 49 　 52 　 55 　 58 　 61 　 64 　67 　 70 　 73 　 76

3 3k-1 　 　 2 　 　 　 5 　 　 　8 　 　 　 11 　 　 　 14 　 　 　 17 　 　 　 20 　 　 　 23 　 　 　 26 　 　 　 29 　 　 　 32 　 　 　 35 　 　 　 38

4 3k-2 　 　 1 　 　 　 　 　 　 4 　 　 　 　 　 　 　 7 　 　 　 　 　 　 　 10 　 　 　 　 　 　 　 13 　 　 　 　 　 　 　16 　 　 　 　 　 　 　 19

5 3k-1 　 　 　 　 　 　 　 　 　2 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 5 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 8

6 3k-2 　 　 　 　 　 　 　 　 　1 4

7 3k-1 2

8 3k-2 1

第一行(2k-1)經過全變換(3(2k-1)+1)/2=3k-1變成第二行,實際上等於第一行加上一個k,其中的奇數5,11,...6k-1又回到了第一行.以下各行是等差數列3k-2,3k-1交錯排列.由於最終都變成了奇數,所以集合O對於變換f(X)是封閉的.

定理二

:任何奇自然數經過若干次變換都會變成1.

證明:

我們看到 奇數經過全變換變成為3k-1型數,3k-1型奇數經過全變換有一半仍然變成3k-1型奇數,而另一半3k-1型偶數經過除以2有一半變成為3k-2型奇數,而3k-2型奇數經過全變換又變成為3k-1型數.換句話說不可能經過全變換得到3k-2型數.

下面我們只研究奇數經過全變換的性質,因為對於其他偶數經過若干次偶變換,仍然要回到奇數的行列里來.

我們首先證明奇數經過若干次全變換必然會在某一步變成偶數.（冰雹猜想又成奇偶變換猜想，“如果偶數除於2“是把偶數變成奇數的運算，偶數歸結於奇數的逆向描述公式是：偶數=f(m,n)=(2n-1)*2^m，這是描述偶數歸結於奇數的另外一個公式。“如果奇數乘於3加1”是把奇數變成偶數 的運算，運用直接歸結定理2個公式描述了)

設2a0-1是我們要研究的奇數,它經過全變換變成3a0-1,假設它是一個奇數並且等於2a1-1,2a1-1又經過全變換變成為3a1-1=2a2-1,3a2-1=2a3-1,...3ak-1-1=2ak-1,所以a1=(3/2)a0,a2=(3/2)a1,...ak=(3/2)ak-1.

所以最後ak=(3/2)ka0,要使ak是整數,可令a0=2kn,(n是奇數).於是ak=3kn.則從2a0-1經過若干次全變換過程如下:

2k+1n-1 -> 3*2kn-1 -> 32*2k-1n-1 -> 33*2k-2n-1 ->... -> 3k+1n-1 (偶數).

然後我們證明經過全變換變成偶數的奇數一定大於該偶數經過若干偶變換之後得到的奇數.

設3k+1n-1=2mh (h為奇數),我們要證明 h<2*3kn-1:

h=(2*3kn-1+3kn)/2m<2*3kn-1,令a=3kn,b=2m-1,則有 2ab>a+b,而這是顯然的.

定義:以下我們將稱呼上述的連續全變換緊接著連續的偶變換的從奇數到另外一個奇數的過程為一個變換鏈.

接著我們證明奇數經過一個變換鏈所得的奇數不可能是變換鏈中的任何中間結果,包括第一個奇數.

若以B(n)表示奇數n的變換次數,m是n經過變換首次遇到的其他奇數,則有。

定理三:B(n)=k+1+B(m),其中k是滿足3n+1=2km的非負整數.

證明:n經過一次奇變換,再經過k次偶變換變成奇數m,得證.

舉例來說,B(15)=2+B(23)=2+2+B(35)=2+2+2+B(53)=2+2+2+5+1+B(5)=2+2+2+5+1+5=17

定理四

按照角谷猜想的擴展部分，每一道擴展的題目都存在著相對應的幾個歸結定理，或者可以叫逆向推算定理，對於原題的文字描述是：文字描述是：首先把自然數中能被3或者是能被2整除的自然數都刪除掉，剩下的自然數，按照第奇數個第偶數個分成2類，其中第奇數個奇數通項公式是：(6（n-1）+1）把這個式子乘於2^（2m）再減去1之後必定可以被3整除，而且得到的自然數全部是奇數。第偶數個奇數的通項公式是：(6(n-1)+5)把這個式子乘於2^（2m-1）再減去1之後必定可以被3整除而且得到的自然數全部都是奇數。這些公式已經被數學歸納法證明成立，該定理的描述範圍是全體奇數，以及3X+1以後的全體偶數。

原題的歸結定理公式描述就是：

((6（n-1）+1)*4^m-1)/3=x1

((6(n-1)+5)*2^(2m-1)-1)/3=x2

這是2個2維平面的變差數列，由2條互相垂直的射線組成的射面狀的無窮變差數列。已經通過數學歸納法證明，公式成立，可以整除，而且得數全部都是奇數。如果把x1和x2都看成是集合，那么必定存在它們的交集必定是空集，它們的並集必定是全體奇數。等於說是把奇數分成2類，一類是x1，另外的一類是x2，再把以上2個式子移項以後就會得到：3x1+1=(6（n-1）+1)*4^m，和3x2+1=(6(n-1)+5)*2^(2m-1)。它們的威力在於，該定理可以描述所有的非最起始點的奇數的3x+1的以前的情況....是逆向的描述....通過這個定理，我們可以非常容易地尋找，不能被3整除的奇數的所有上一步的直接歸結的情況。這個直接歸結定理在分析冰雹猜想的過程中發揮著非常重要的作用。假設我被邀請去參加某次的數學成果研究大會，站在講台上我就可以說任意給我一個不能被3整除的奇數我都能馬上算出，它所有上一步的奇數，也就是在忽略偶數不記錄的前提下的所有直接歸結於這個奇數的奇數。文字描述是：首先把自然數中能被3或者是能被2整除的自然數都刪除掉，剩下的自然數，按照第奇數個第偶數個分成2類，其中第奇數個奇數通項公式是：(6（n-1）+1）把這個式子乘於2^（2m）再減去1之後必定可以被3整除，而且得數是全部奇數。第偶數個奇數的通項公式是：(6(n-1)+5)把這個式子乘於2^（2m-1）再減去1之後必定可以被3整除而且得數全部都是奇數。

x1交x2=空集

x1並x2=全體奇數

正是因為它們是全體奇數所以這個定理在證明過程中無處不在.............

同時對於任意任何一個能被3整除的奇數，都絕對不存在上一步的奇數，都是順冰雹猜想驗證的最起始點的奇數，都是逆向冰雹猜想的終止點的奇數，跟最主歸結點的1的情況剛好相反的.

原始克拉茨

二十世紀30年代,克拉茨還在上大學的時候,受到一些著名的數學家影響,對於數論函式發生了興趣,為此研究了有關函式的疊代問題.

在1932年7月1日的筆記本中,他研究了這樣一個函式:

F(x)= 2x/3 （如果x被3整除 或者 (4x-1)/3 （如果x被3除餘1）或者 (4x+1)/3 （如果x被3除餘2）

則F(1)=1,F(2)=3,F(3)=2,F(4)=5,F(5)=7,F(6)=4,F(7)=9,F(8)=11,F(9)=6,...為了便於觀察上述疊代結果,我們將它們寫成置換的形式:

1 2 3 4 5 6 7 8 9 ...

1 3 2 5 7 4 9 11 6 ...

由此觀察到:對於x=2,3的F疊代產生循環(2,3)

對於x=4,5,6,7,9的F疊代產生循環(5,7,9,6,4).

接下來就是對x=8進行疊代,克拉茨在這裡遇到了困難,他不能確知,這個疊代是否會形成循環,也不知道對全體自然數做疊代除了得到上述兩個循環之外,是否還會產生其他循環.後人將這個問題稱為原始克拉茨問題.人們更感興趣的是它的逆問題:

G(x)= 3x/2 （如果x是偶數）或者 (3x+1)/4 （如果x被4除餘1）或者 (3x-1)/4 （如果x被4除餘3）

不難證明,G(x)恰是原始克拉茨函式F(x)的反函式.對於任何正整數x做G疊代,會有什麼樣的結果呢?

經計算,已經得到下列四個循環:

(1),(2,3),(4,6,9,7,5),(44,66,99,74,111,83,62,93,70,105,79,59).

因為G疊代與F疊代是互逆的,由此知道,F疊代還應有循環(59,79,105,70,93,62,83,111,74,99,66,44).

G疊代還能有別的循環嗎?為了找到別的循環,人們想到了下面的巧妙方法:

由於G疊代使後項是前項的3/2(當前項是偶數時)或近似的3/4(當前項是奇數).如果G疊代中出現循環,比如疊代的第t項at與第s項as重複(t<s):at=as.但

as/as-1,as-1/as-2,...at+1/at

或等於3/2,或者近似於3/22,因而

1=as/at=as/as-1*as-1/as-2*...at+1/at≈3m/2n

這裡 m=s-t,m < n

即 2n≈3m

log22n≈log23m

故 n/m≈log23

這就是說,為了尋找出有重複的項(即有循環),應求出log23的漸進分數n/m,且m可能是一個循環所包含的數的個數,即循環的長度.

log23展開成連分數後,可得到下列緊缺度不同的漸進分數:

log23≈2/1,3/2,8/5,19/12,65/41,84/53,485/306,1054/665,24727/15601,...

漸進分數2/1表明,31≈22,循環長度應為1.實際上恰存在長度為1的循環(1).

漸進分數3/2表明,32≈23,循環長度應為2.實際上恰存在長度為2的循環(2,3).

漸進分數8/5表明,35≈28,循環長度應為5.實際上恰存在長度為5的循環(4,6,9,7,5).

漸進分數19/12表明,312≈219,循環長度應為12,實際上恰存在長度為12的循環(44,66,...59).

這四個漸進分數的分母與實際存在的循環長度的一致性,給了人們一些啟發與信心,促使人們繼續考慮:是否存在長度為41,53,306,665,15601,...的循環?令人遺憾的是,已經證明長度是41,53,306的循環肯定不存在,那么,是否會有長度為665,15601,...的循環呢?

F疊代與G疊代究竟能有哪些循環呢?人們正在努力探索中！

代數學原理：

整數環Z上的3n+1代數結構由有理數域Q上的3n+d伽羅瓦置換群定義，因此Z/Q=1/3，CQZ/Q=2/3：即3n+d群在Z上的封閉域為1/3，在Q上的擴張域為2/3，因此可知Z上的3n+1奇偶性變換具有唯一性，可通過Q上的3n+d置換群的自同構來構造出Z上的3n+1循環群

證明：

對有理函式f=F(d，n)=3n+d，(d，n)∈Q進行路徑積分： 構造有理域變換: f: Q→Q: L⇆J⇆A⇆B，F=(x，y，z)={∑f(x，y，z)|x=3n+d，y=3n-d，z=n/2，(d，n)∈Q}:

函式f(d,n)在複平面內的分形圖，黑洞為有理域，藍色為無理域

⇆L=(x0，y0，z0)={∑f(x0，y0，z0)|d=0，n=0，x0=3×0+0=0，y0=3×0-0=0，z0=0/2=0}

⇆J=（x1，y1，z1）={∑f(x1，y1，z1)|d=1，n=0，x1=3×0+1=1，y1=3×0-1=-1，z1=0/2=0}

⇆A=(x2，y2，z2)={∑f(x2，y2，z2)|d∈Q，n∈Q+，x2=3×1+d，y2=3×1-d，z2=n/2}

⇆B=(x3，y3，z3)={∑f(x3，y3，z3)|d∈Q，n∈Q-，x3=3×(-1)+d，y3=3×(-1)-d，z3=n/2}。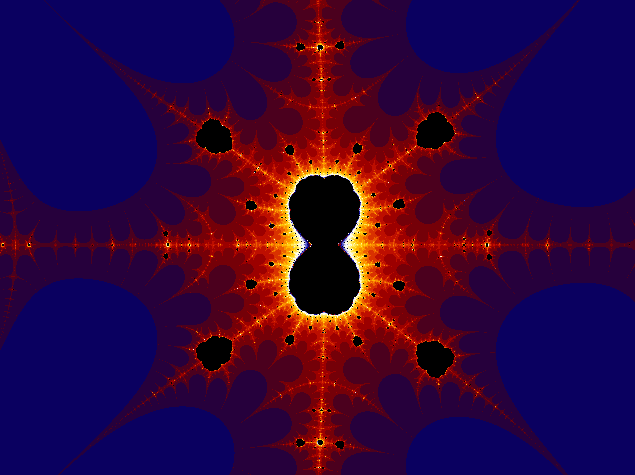

核心黑洞為整環，繞核黑洞為整環衍生的有理分式域

(1)通過路徑A進行有理域變換：

【1】(3×1+d1-1)/3=(3×1-d1)/2，

d1=1；

(3×1-d2-1)/3=(3×1+d2)/2，

d2=-1。

【2】(3×1-d3)/2=2(3×1+d3)，

d3=9/5；

(3×1+d4)/2=2(3×1-d4)，

d4=-9/5。

【3】3(3×1-d5)+1=2(3×1+d5)，

d5=4/5；

3(3×1+d6)+1=2(3×1-d6)，

d6=-4/5。

取d=1，則x2=4，y2=2，可得拓撲循環A=(4，2，1，4)。根據變換法則，取拓撲不動點n=1，則x4=3×1+1=4，y4=3×1-1=2，可得拓撲循環S=(4，2，1，4)=A，所以S同胚於A，因此可得拓撲循環(A，A)，所以A是單連通域，因此正整環上的3n+1變換有且只有拓撲循環：(A⇆A)。

交接處的尖點為拓撲不動點，即兩個黑洞的作用奇點

(2)通過路徑B進行有理域變換：

〈1〉由(1)可知n=-1時本變換等價於(1)，因此d=1，x5=-2，y5=-4，可得拓撲循環B=(-1，-2，-1)，因為-4∉B，所以n=-1不是拓撲不動點，不滿足變換法則，因此取拓撲不動點n=-2。

〈2〉

【1】[3×(-2)-d7-1]/3=[3×(-2)+d7]/2,

d7=4/5；

[3×(-2)+d8-1]/3=[3×(-2)-d8]/2，

d8=-4/5。

【2】[3×(-2)-d9]/2=2[3×(-2)+d9]，

d9=18/5；

[3×(-2)+d10]/2=2[3×(-2)-d10]，

d10=-18/5

【3】3[3×(-2)+d11]+1=2[3×(-2)-d11],

d11=1；

3[3×(-2)-d12]+1=2[3×(-2)+d12]，

d12=-1。

取d=1，則x6=-5，y6=-7，可得拓撲循環C=(-5，-14，-7，-20，-10，-5)，根據變換法則，取拓撲不動點n=-14。

〈3〉

【1】[3×(-14)-d13-1]/3=[3×(-14)+d13]/2,

d13=8；

[3×(-14)+d14-1]/3=[3×(-14)-d14]/2，

d14=-8。

【2】[3×(-14)-d15]/2=2[3×(-14)+d15],

d15=126/5；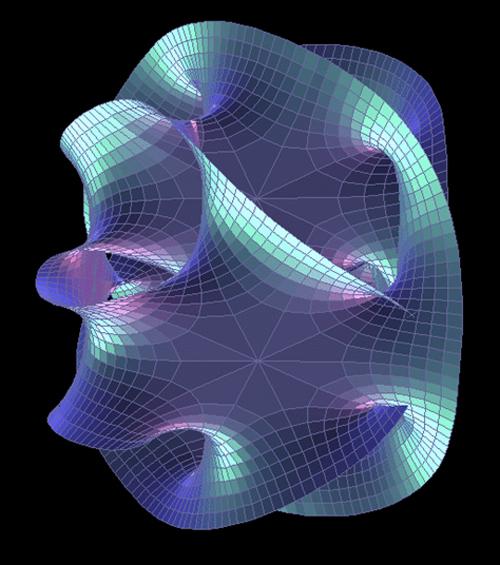

函式f(d,n)無窮自同構後生成的無限次迴繞的高維空間

[3×(-14)+d16]/2=2[3×(-14)-d16]，

d16=-126/5。

【3】3[3×(-14)+d17]+1=2×[3×(-14)-d17]，

d17=41/5；

3[3×(-14)-d18]+1=2[3×(-14)+d18]，

d18=-41/5。

取d=8，則x7=-34，y7=-50，可得拓撲循環D=(-34，-17，-50，-25，-74，-37，-110，-55，-164，-82，-41，-122，-61，-182，-91，-272，-136，-68，-34)，根據變換法則，取拓撲不動點n=-17。

〈4〉

【1】[3×(-17)-d19-1]/3=[3×(-17)+d19]/2，

d19=49/5；

[3×(-17)+d20-1]/3=[3×(-17)-d20]/2，

d20=-49/5。

【2】[3×(-17)-d21]/2=2[3×(-17)+d21]，

d21=153/5；

[3×(-17)+d22]/2=2[3×(-17)-d22]，

d22=-153/5。

【3】3[3×(-17)+d23]+1=2[3×(-17)-d23]，

d23=10；

3[3×(-17)-d24]+1=2[3×(-17)+d24]，

d24=-10。

取d=10，則x8=-41，y8=-61，可得拓撲循環E=(-41，-122，-61，……，-41)=D，所以E同胚於D，因此可得拓撲循環(D，D)，所以D是單連通域，因此B，C，D兩兩同倫，所以負整環上的3n+1變換有3個拓撲循環：(B⇆B)⇆(C⇆C)⇆(D⇆D)。

綜上所述，整環上的3n+1變換有5個拓撲循環，其中0被定義為偶數，(0⇆0)為奇異拓撲循環，則有：(A⇆A)⇆(0⇆0)⇆(B⇆B)⇆(C⇆C)⇆(D⇆D)。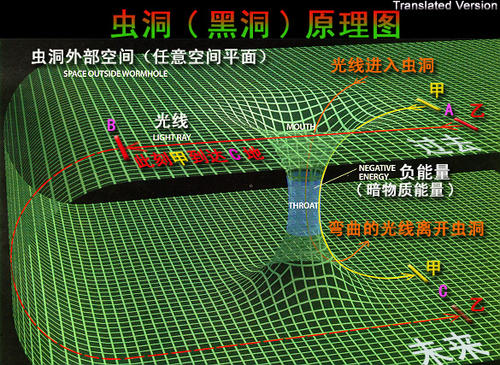

不同黑洞之間通過蟲洞連通起來實現瞬間時空穿越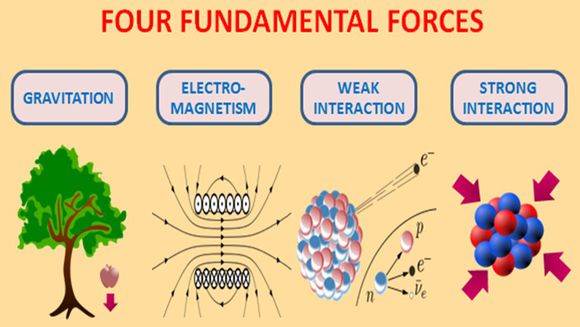

萬有引力，電磁力，弱力，強力在黑洞處統一

磁單極子對稱，磁雙極子對稱破缺，磁雙極子真空激發成磁單極子

電子從原子高能級軌道向低能級軌道躍遷時釋放和吸收能量

六種夸克每3種組成一種質子，2種質子+電子分別組成物質與反物質

不同黑洞通過物質與反物質相互結合泯滅成真空零點能相互作用

函式f(d,n)自同構形成三維黎曼曲面，交叉線由拓撲不動點集合形成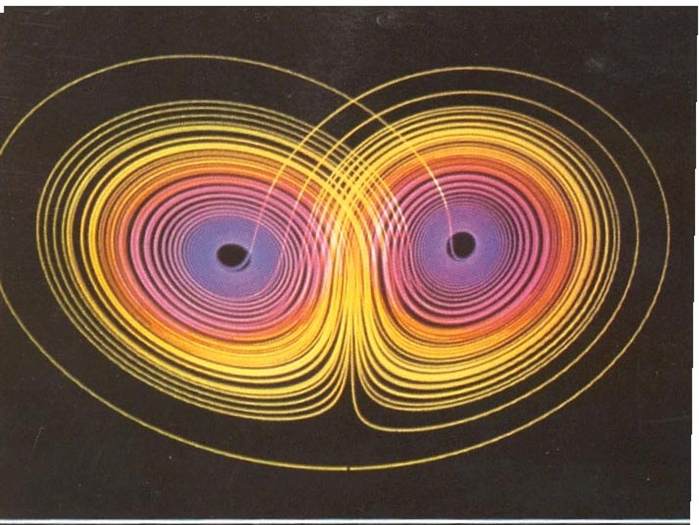

函式f(d,n)的自同構過程本質上是一對無限次來迴環繞的雙黑洞系統

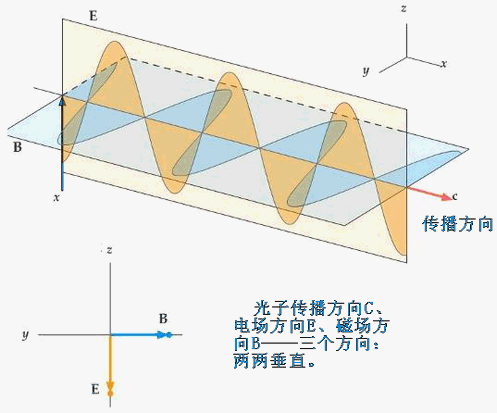光的傳播路徑形象地演繹了函式f(d,n)的自同構模型：三維正交

Java驗證實現import java.util.Scanner;public class JiaoGuCaiXiang {public static void main(String[] args) {Scanner sc=new Scanner(System.in);System.out.print("請輸入要進行判斷的數字：");int a=sc.nextInt();jiaogu(a);}public static void jiaogu(int a){if(a>1){if (a%2==0) {a=a/2;System.out.println("偶數的變化是"+a);}else{a=3*a+1;System.out.println("奇數的變化是"+a);}}else{return;}jiaogu(a);}}=============c++驗證實現=============#include <iostream>using namespace std;int main (){   int array[1000];//n的值無法預估。   int n = 0;   cout << "input the first number of Hailstone" << endl;//輸入第一個數字   cin >> array[n];   cout << "array [ "<< n <<"] = " << array[n] << endl;   while (array[n] != 1)   {      if(array[n]%2)             {                 array[n+1] = array[n]*3 + 1;                 n++;                 cout << "array [ "<< n <<" ] = " << array[n] << endl;             }      else             {                 array[n+1] = array[n]/2;                 n++;                 cout << "array [ "<< n <<" ] = " << array[n] << endl;             }   }   cout << "n = " << n << endl;   return 0;}=============C語言實現=============#include <stdio.h>//use whileint bingbao(unsigned long  a ){    int ret=0;    while(a!=1)    {        if (a%2)        {            a=a*3+1;                    }        else         {            a=a/2;        }        printf("%ld\n",a );        ret++;    }    return ret;}//遞歸法。void bingbao2(unsigned long n){    printf("%ld\n",n);    if(n!=1)    {        unsigned long newValue;        if(n%2)        {            newValue=n*3+1;        }        else        {                        newValue=n/2;        }        bingbao2(newValue);            }}int main(int argc, char const *argv[]){    unsigned long  a;    int b;    printf("please input a number.\n");    scanf("%ld",&a);        b=bingbao(a);    printf("times=%d\n",b );    bingbao2(a);        return 0;}=============JS語言實現=============function hailGuess(n) {  const originNum = n  if (!Number.isInteger(n) || n === 0) {    throw new Error('arguments is invaild')  }  let result = [n]  while(n !== 1) {    if (n % 2 === 0) {      n /= 2    } else {      n = 3 * n + 1    }    result.push(n)  }  console.log(`test value is ${originNum},\nresult length is ${result.length - 1} steps,\nresult Quene is: ${result}. \n`)  return result}=============Python語言實現=============def collatz(number):        if number % 2 == 0:                print(number // 2)                return number // 2         elif number % 2 == 1:                 print( 3 * number + 1)                 return 3* number + 1         else:                 print('Please have a right input')amazing = int(input('input a number: '))     while collatz(amazing) != 1:         amazing = collatz(amazing)