基本介紹
- 中文名:擬素數
- 外文名:擬素數
- 英文:uasi prime number
- 原始的:素性檢驗思想就是檢驗
定義,性質,算法,
定義
常用的擬素數有以下幾種:

成立,則 叫做基於
叫做基於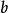 的擬素數。
的擬素數。

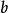

則稱 為基於
為基於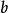 的Euler擬素數。(其中
的Euler擬素數。(其中 表示
表示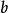 關於
關於 的Jacobi符號)
的Jacobi符號)

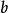

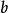

3、強擬素數:設 為正的奇合數,且滿足
為正的奇合數,且滿足 ,其中
,其中 為奇數。
為奇數。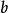 與
與 互素,若有以下關係成立:
互素,若有以下關係成立:



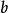

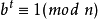
或者存在一個整數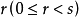 使得:
使得:
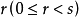

則 叫做基於
叫做基於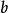 的強擬素數。
的強擬素數。

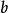
性質
定理1:存在無窮多個擬素數,Euler擬素數和強擬素數。
證明概要:只需證明如果 為擬素數,則
為擬素數,則 為強擬素數即可。
為強擬素數即可。


定理2:如果一個數 是基於
是基於 的Euler擬素數,那么它也是基於
的Euler擬素數,那么它也是基於 的擬素數。
的擬素數。



證明:顯然。
定理3:如果一個數 是基於
是基於 強擬素數,那么它也是基於
強擬素數,那么它也是基於 的Euler擬素數。
的Euler擬素數。



證明:令 為基於
為基於 的強擬素數,則其可分解為
的強擬素數,則其可分解為 (允許重複)。定義
(允許重複)。定義 使得
使得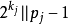 並且假定
並且假定 。由
。由 為強擬素數知,存在k使得
為強擬素數知,存在k使得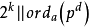 對任意
對任意 均滿足(k即為
均滿足(k即為 關於
關於 的指數所包含的因子2的個數)。因此有
的指數所包含的因子2的個數)。因此有 ,令
,令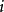 表示
表示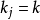 的個數,那么有
的個數,那么有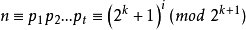




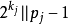


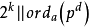




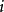
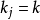
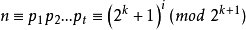
所以 或
或 取決於
取決於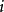 是奇數還是偶數。所以
是奇數還是偶數。所以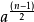 ≡-1或1(mod
≡-1或1(mod  )取決於
)取決於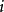 是奇還是偶。
是奇還是偶。


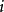
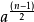

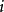
另一方面,若 那么
那么 ,若
,若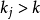 則有
則有 。
。


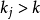

所以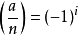 ,因此也取決於
,因此也取決於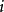 的奇偶性。所以
的奇偶性。所以 ,即
,即 也為基於
也為基於 的Euler擬素數。
的Euler擬素數。
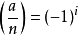
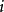



算法
通過如上三種擬素數的定義,可以直接導出三種素性檢驗的方法,分別為:Fermat素性檢驗、Solovay-Stassen素性檢驗(基於Euler擬素數)、Miller-Rabin素性檢驗(基於強擬素數)。可以證明前兩者檢測出n為合數的機率不小於50%,後者檢測出來的機率不小於75%。
